Le contenu de ce cours de 2ème année de Licence, développé en 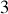grains, considère comme acquise la mécanique vectorielle du point matériel (particule élémentaire).

Néanmoins des rappels et compléments sont proposés dans ce premier grain.

L'objectif final est de traiter la mécanique du solide. L'extension au problème à N corps est alors effectuée dès que possible.

De ce fait, la généralisation au système de points apparaît naturellement, pointant ses particularités.

Ce cheminement vers la complexité s'accompagne d'une formalisation progressivement plus complexe mais également diverse.

En effet, les théories utilisées répondent aux besoins de la description et s'adaptent à ses hypothèses.

• Le déroulement de ce cours suivra une approche interrogative, un questionnement tous azimuts, car aussi bien la formulation lagrangienne (grain 2) que la mécanique des solides (grain 3) nécessitent une réflexion particulière : plus analytique, plus énergétique.

Des compléments comparatifs entre formalismes vectoriel et énergétique seront ainsi particulièrement développés en vue d'une application aux systèmes complexes.

Différentes définitions seront explicitées et généralisées selon l'approche et le formalisme utilisés.

Applications, exemples et exercices seront ainsi abordées avec l'une ou l'autre des formulations, en fonction de l'objectif pédagogique et du niveau de complexité.

Finalement toutes les applications seront traitées avec au moins deux méthodes, chacune apportant ses éléments d'investigation, d'interprétation et de compréhension.

Une réponse incomplète, dans un exemple, constitue souvent un début ou un élément de réponse dans un autre.

• Il s'agit, à priori, d'un cours basé sur des valeurs typiquement universitaires dont la finalité première est une acquisition d'autonomie par l'étudiant.

  Ce cours associe la liberté de décrire progressivement un système physique, à celle de l'analyser, raisonner pour reconstruire la complexité propre du système ; le tout balisé par la rigueur scientifique.

La phase d'analyse permet souvent de faire le point sur ce qui est acquis, puis d'ouvrir des portes, des perspectives.

Une arborescence qui se construit du plus simple vers le plus compliqué.

L'intérêt de ce grain réside dans cette approche interrogative, plus que dans son contenu : les problèmes posés sont partout résolus et le contenu existe dans tout bon livre de mécanique.

En plus d'évoluer vers des systèmes de plus en plus complexes, cette approche met simultanément en place un comparatif des modélisations (ou descriptions) pour faire le tour des capacités de chacune à apporter quelques réponses aux questions.

Tout problème trouve sa solution, tributaires de ses hypothèses.

Elle peut être partielle selon la théorie.

En effet, les modélisations mises en œuvre portent en elles leurs propres limites.

Et ces limites situent les "nœuds" du raisonnement et les invalidités.

Elles peuvent même donner des indications sur les erreurs commises dans l'application du modèle ou des voies de contournement des difficultés.

Cette démarche est ainsi appliquée au second grain et permet la découverte pas à pas du formalisme lagrangien.

Dans le dernier et troisième grain, sont généralisées et appliquées aux systèmes "solides" les descriptions développées dans les grains 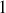et 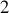: ces systèmes ont une richesse qui permet des variations.

• Comment construire une théorie ? Quelles analogies avec d'autres domaines de la physique ?

La pluridisciplinarité de la Physique a produit un fractionnement quasi inévitable de son enseignement.

Et la Mécanique, au sein de la Physique, contient une forme de transversalité, probablement due à son origine, à son histoire.

Elle s'ouvre aisément vers les autres domaines : des vibrations vers les ondes et l'optique, des charges vers les liaisons chimiques, l'énergétique ou l'électronique, de l'infiniment grand vers l'infiniment petit...

Ce cours est un cours de Mécanique Physique.

L'un de ses buts est de mettre en valeur l'unité de la Physique autour d'une approche associant l'expérience, un mode d'analyse, des méthodes et pratiques, le tout indissociable de la modélisation.

Soumis aux aléas

- des générations d'étudiants et de leurs questions,

- de réformes successives soumises à des modes de pensée,

ce cours est devenu un cheminement à travers les règles et autour des lois de la Physique.

Ainsi cet enseignement essaie de répondre à des questions d'étudiants portant le plus souvent sur la mathématisation (mise en équations) des problèmes que sur les phénomènes eux-mêmes.

L'un des objectifs est donc de s'atteler à la ‘matérialisation' des fondamentaux mathématiques et au développement du sens physique, souvent multiple, qu'il faut y associer.

Le "pourquoi" de la compréhension permet souvent de renforcer voire d'orienter le cheminement du "comment"... des recettes utilisées.

La modélisation est ainsi la voie la mieux adaptée pour atteindre cet objectif.

Et la Mécanique, de toutes les dimensions de la Physique, est celle qui s'y prête le mieux.

Les outils mathématiques feront ainsi l'objet de rappels succincts et de renvois circonstanciés mais souvent obligatoires, avant et pendant les exemples et exercices.

Ces rappels "utilitaires" et leur manipulation sont aussi importants pour les démonstrations de cours que pour les applications.

A la fin de cet avant-propos, un point de vue personnel : comme pour un cours sur papier, il manquera à ce cours numérique une voix, des intonations, et donc des convictions.

Mais cela, c'est en soi qu'on les trouve : après des analyses, comparaisons et longues réflexions.

Après un travail personnel dont les doutes et certitudes sont à croiser avec ceux des autres.

Un principe universitaire.

Et plus probablement universel.