Considérons maintenant le même problème que précédemment mais avec un pendule vertical (figure 5). Le système étudié est la masse, le référentiel
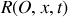 et les forces extérieures appliquées
et les forces extérieures appliquées
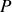 et
et
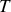 . A l'équilibre, le poids compense la tension du ressort et l'on a:
. A l'équilibre, le poids compense la tension du ressort et l'on a:
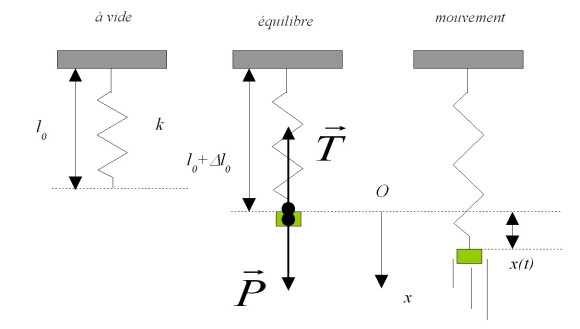
Figure 5 : Représentation d'un pendule élastique vertical ; nous convenons de choisir l'origine O de l'axe des x à la position d'équilibre de ressort.
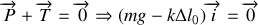
En mouvement, le poids ne compense plus la tension. L'origine
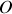 du mouvement est prise sur la position d'équilibre du ressort. L'application de la
du mouvement est prise sur la position d'équilibre du ressort. L'application de la
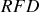 conduit à:
conduit à:
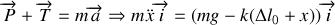
En utilisant la condition d'équilibre du ressort, on aboutit à l'équation différentielle du mouvement du pendule élastique :
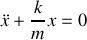
Remarque :
Le mouvement a les mêmes caractéristiques que pour l'oscillateur horizontal.



