Introduction
Le solide est un cas particulier de systèmes constitués d'un grand nombre de particules.
L'étude de son mouvement dans l'espace est caractérisée par une réduction significative du nombre de variables comparativement au problème à
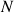corps.
Le solide peut être déformable ou indéformable (rigide).
Le solide indéformable est le plus simple des systèmes complexes : le nombre de particules situées à distances fixes les unes des autres étant infini, ces contraintes apportent une simplification notable au traitement du système de points.
L'étude du mouvement du solide indéformable permet néanmoins la mise en place de quelques outils de base pour décrire des systèmes plus complexes. En effet, cette étude représente une seconde étape, après celle du point matériel, vers la description du cas général à N corps en passant par les systèmes solides déformables (articulés notamment) et les milieux continus.
Un solide, sous entendu indéformable, évolue en général dans l'espace à
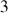dimensions et sa rigidité rend inutile le suivi séparé de chaque point constituant le solide.
Un outil de description qui caractérise tout système de points (
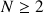), quel qu'il soit, provient de l'existence du point particulier, aux propriétés multiples : c'est le barycentre ou centre de masse (CDM) ou d'inertie (CdI) ou de gravité (CdG), une dénomination selon le contexte.
Dans le cas du solide, ce point a une position fixe dans le solide et permet de visualiser certaines symétries.
Partant de là, un schéma en deux étapes apparaît :
Décrire le mouvement de ce point, fixe dans la structure solide, constitue une description partielle du mouvement du solide et qui, de fait, correspond à l'approximation du point matériel tout en décrivant le mouvement global (d'ensemble) du solide.
Tous les autres points étant fixes, par rapport au CDM, il reste alors à étudier leur position relative... : le complément de description est développée (et ‘tournera') autour de ce point.
A l'opposé et dans le cas d'un solide déformable, la position du CDM varie avec la déformation entraînant une variation relative par rapport aux autres points du solide.
La méthode d'analyse du mouvement du solide ne peut être appliquée telle que décrite dans ce grain.
Mais certaines contraintes (par exemple, celles d'une chaîne sur le bord d'une table) produisent des phases, temporelles et/ou spatiales, telles qu'un traitement partiel est possible par la mécanique du solide, qui alors peut donner des indications sur la démarche à suivre.
L'application des lois de la mécanique dans une démarche variationnelle ou fractionnée prouve l'intérêt de rester au plus près de la description d'un point matériel utile et d'identifier les compléments.
Le solide peut être décrit par des grandeurs intrinsèques, indépendantes du référentiel choisi et tributaires de ses symétries.
Ces grandeurs constituent l'ossature autour de laquelle se construit la dynamique de son mouvement et par conséquent, l'élaboration de ce cours.
Elles sont au nombre de deux.
Le centre d'inertie ou de masse (CDM) dans le cas général, dont le mouvement est analysé.
Mais d'autres points du solide peuvent jouer un rôle similaire à celui du CDM.
La seconde caractéristique générale du solide provient de ses rotations lesquelles impliquent des variables angulaires et surtout des axes de rotation en relation avec ses symétries.
Les rotations constituent souvent des grandeurs à déterminer.
La description du mouvement des solides portera donc sur une décomposition des mouvements autour de ces deux entités, préalablement définies.
Ce mouvement est donc caractéristique d'une composition de
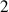types de mouvement.
Le cours sera élaboré en séparant les deux éléments suivants :
Le traitement du mouvement du CDM, lequel revient à celui du mouvement d'un point matériel.
Les rotations, par contre, nécessitent une familiarisation préalable qui passe par l'élaboration d'outils adaptés et les principes de leur utilisation.
Ainsi dans un premier temps, le moment cinétique (ou moment angulaire), le moment d'inertie par rapport à un axe et la simple rotation autour de cet axe seront explicités.
Chacun de ces deux mouvements nécessite une représentation dans l'espace :
La rotation totale est le résultat d'au plus
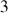rotations.Le vecteur vitesse angulaire
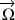est porté par un axe de rotation. Dans l'espace et dans le cas général, ce vecteur comportera trois composantes dans un référentiel d'axes mobiles, fixé au solide et qui le caractérisera.
La description de la rotation utilisera, en plus, un référentiel lié au solide mais d'axes fixes, permettant ainsi d'initialiser la rotation du solide.
Le mouvement global est pris en compte par l'utilisation d'un référentiel fixe, celui du laboratoire par exemple.
Le centre, et les axes, de ce repère seront les références pour la translation globale du solide et sa rotation, respectivement.
En résumé, des descriptions dans
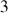différents référentiels, dont
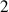sont liés au solide et
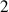ont des axes de directions fixes, sont nécessaires.
Finalement, décrire le mouvement d'un solide nécessitera une reconstruction autour d'une composition de mouvements.
Mais avant cela, la formulation la plus générale qui soit de la rotation dans l'espace sera présentée : il s'agit de la rotation vectorielle utilisant les trois rotations d'Euler.
L'intérêt premier de la vitesse de rotation proposée par Euler est de fournir une base standard de rotations par rapport à laquelle les rotations naturelles et réelles seront identifiées.
Ce cours respecte l'approche explicitée dans les grains antérieurs, consacrés aux bases de la mécanique physique et au formalisme de Lagrange, construits sur
un questionnement pas à pas, ce qui produit des redites : la démarche rationnelle suit des règles et donc des cheminements parallèles.
une évolution progressive vers la complexité même si les exemples traités dans ce cours sont simples.
La plupart des définitions et outils utilisés dans ce cours ont été déjà mis en place dans les cours antérieurs en prévision de leur utilisation dans le problème à
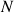corps.
Ce cours sera construit avec des allers-retours entre formalisme vectoriel appliqué aux solides et formalisme lagrangien, d'où la nécessité de maîtriser ces deux volets explorés dans les deux grains précédents et exploités dans celui-ci.
