Envisageons l'écoulement stationnaire () d'un fluide parfait () incompressible (). L'équation de Navier-Stokes précédemment établie se simplifie de la manière suivante :

Par ailleurs, si l'accélération de la pesanteur peut être considérée constante et telle que , alors on peut formuler l'équivalence suivante :

ce qui permet de regrouper ainsi les deux gradients :

D'un point de vue purement mathématique, le terme de gauche (l'accélération convective) peut être développée de la manière suivante :

et conduit à cette nouvelle formulation de l'équation de Navier-Stokes :

On identifie alors la présence du vecteur tourbillon et donc :

Cette dernière formulation permet d'en déduire que si l'écoulement est irrotationnel, alors :

signifiant que la quantité est indépendante des coordonnées de l'espace. Ainsi, pour résumer, l'écoulement stationnaire et irrotationnel d'un fluide parfait est caractérisé par :

en tout point de l'écoulement.

Faisons maintenant appel à la notion de ligne de courant : il s'agit d'une courbe qui, en chacun de ses points, est tangente au vecteur vitesse. On notera que dans le cas particulier d'un écoulement stationnaire, le champ de vecteurs vitesse étant statique, les lignes de courant sont également statiques et, de fait, sont équivalentes aux trajectoires des particules (voir cours portant sur la cinématique des fluides).

Figure 18

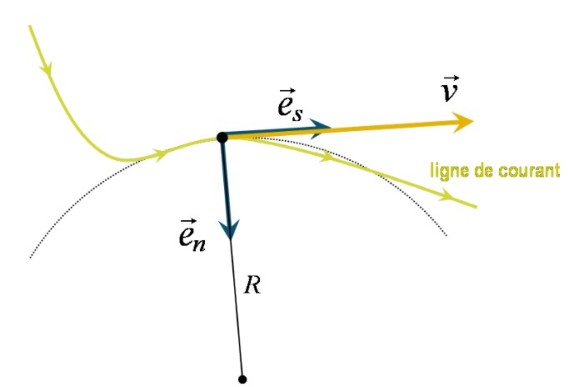
En un point d'une ligne de courant, le vecteur vitesse étant tangent, il présente une seule composante non nulle dans le repère de Frenet associé au point (voir figure 18) :

où est la norme du vecteur vitesse. Dans ce même repère, l'opérateur gradient présente les deux composantes suivantes :

Décomposons l'opérateur dans ce repère :

Il s'ensuit :

Sachant que où est le rayon de courbure de la ligne de courant au point considéré, il vient :

Par identification des composantes selon et , on doit vérifier le long d'une ligne de courant :

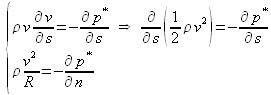
La seconde équation montre d'une part que , traduisant le fait que la pression motrice diminue lorsqu'on se rapproche du centre de courbure. D'autre part, on en déduit que pour un faisceau de lignes de courant rectilignes et parallèles, le centre de courbure étant projeté à l'infini, la pression motrice ne varie pas transversalement : perpendiculairement aux lignes de courant rectilignes (ce qui revient à appliquer la loi fondamentale de l'hydrostatique).

La première équation peut aussi se rassembler sous la forme :

traduisant le fait que reste constant le long d'une même ligne de courant.

De manière très générale, cette équation de Bernoulli traduit le principe de conservation de l'énergie le long d'une ligne de courant dans le cadre de l'écoulement d'un fluide parfait. En effet, multiplié par un volume unitaire, chacun des termes de l'équation a la dimension d'une énergie :

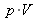• correspond au travail des forces de pression ; c'est ainsi l'énergie potentielle due aux forces de pression statique ;

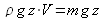• correspond à l'énergie potentielle due aux forces de pesanteur ;

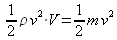• correspond à l'énergie cinétique.

La somme de ces trois énergies s'identifie donc à l'énergie mécanique, laquelle est conservée le long d'une ligne de courant. Autrement dit, l'absence de frottement dû à une viscosité négligée (fluide parfait) conduit logiquement au fait qu'il n'y a pas de dissipation d'énergie au cours de l'écoulement. On entrevoit alors, par déduction, que l'écoulement d'un fluide réel (visqueux) sera caractérisé par une diminution progressive de l'énergie mécanique (voir chapitre à venir concernant les pertes de charge régulières).