Gardant à l'esprit que l'équation de Bernoulli établie précédemment s'applique dans un cadre restreint (écoulement stationnaire d'un fluide incompressible non visqueux), il est néanmoins possible de l'utiliser pour décrire le fonctionnement d'un certain nombre d'applications concrètes ou de phénomènes naturels sur lesquels s'appuient certains dispositifs technologiques.
Parmi ces applications, nous proposons ici d'en détailler quelques unes, choisies pour leur simplicité et leur caractère édifiant : le tube de Pitot, permettant une mesure de la vitesse d'écoulement ; l'effet Venturi, sur lequel repose le principe d'une mesure de débit en conduite ; la caractérisation de la vidange d'un réservoir (formule de Torricelli) ; l'origine du phénomène de cavitation.
Tube de Pitot
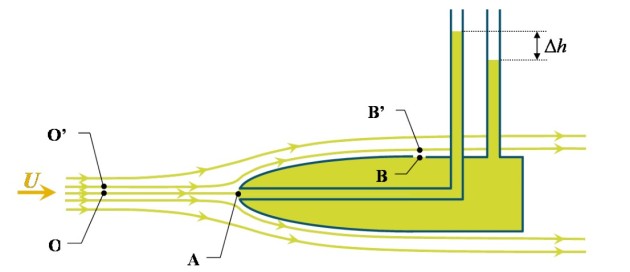
Dans son principe, il s'agit d'un dispositif extrêmement simple qui permet une mesure de la vitesse d'écoulement d'un fluide. L'objet présente une forme profilée, est creux afin d'être rempli du fluide dans lequel il est immergé, et doit être muni de deux prises de pression (tubes manométriques). Comme le montre le schéma de la figure 19, l'un des deux tubes manométriques est relié au front d'attaque de l'objet (point d'arrêt caractérisé par une vitesse d'écoulement nulle), alors que l'autre est en prise avec le fluide statique remplissant l'objet.
En supposant que le fluide est non visqueux, incompressible et que l'écoulement est stationnaire et uniforme en amont de l'objet, on va pouvoir identifier un certain nombre de lignes de courant et y appliquer l'équation de Bernoulli. On supposera par ailleurs que toutes ces lignes de courant sont approximativement à la même altitude.
Le long de la ligne de courant passant par le point d'arrêt A et le point O, on a :
![]() , avec
, avec ![]() ,
, ![]() et
et ![]() .
.
Par conséquent, on obtient la pression de stagnation : ![]() , où
, où ![]() et
et ![]() sont respectivement la pression et la vitesse de l'écoulement uniforme (écoulement amont, non perturbé par la présence de l'objet sonde). Par application de la loi de l'hydrostatique, cette pression de stagnation est liée au niveau affiché dans le premier tube manométrique.
sont respectivement la pression et la vitesse de l'écoulement uniforme (écoulement amont, non perturbé par la présence de l'objet sonde). Par application de la loi de l'hydrostatique, cette pression de stagnation est liée au niveau affiché dans le premier tube manométrique.
Le long de la ligne de courant passant par les points O' et B', on a :
Les points O et O' étant infiniment proches, on peut considérer que ![]() et
et ![]() ; d'autre part, le point B' est situé dans une zone où l'écoulement redevient uniforme (les lignes de courant redeviennent rectilignes et parallèles) : il s'ensuit que
; d'autre part, le point B' est situé dans une zone où l'écoulement redevient uniforme (les lignes de courant redeviennent rectilignes et parallèles) : il s'ensuit que ![]() , et l'équation de Bernoulli se résume à :
, et l'équation de Bernoulli se résume à : ![]() .
.
Le point B est situé au niveau de l'orifice permettant au dispositif d'être rempli par le fluide. En conséquence, la pression en B est la même que celle qui règne de manière uniforme à l'intérieur et qui est mesurée par le second tube manométrique. Par ailleurs, puisqu'à l'aplomb du point B, les lignes de courant sont rectilignes et parallèles, la loi de l'hydrostatique s'applique pour donner :
![]() , avec
, avec ![]() . Ce qui conduit simplement à
. Ce qui conduit simplement à ![]() .
.
Pour résumer, on vient de montrer que ![]() et
et ![]() . Or, la différence de niveau
. Or, la différence de niveau ![]() lue grâce aux deux tubes manométriques permet d'évaluer la différence de pression entre les points A et B :
lue grâce aux deux tubes manométriques permet d'évaluer la différence de pression entre les points A et B :
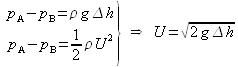
Il en résulte que ce dispositif permet une mesure quasi directe de la vitesse d'écoulement uniforme.
Remarque :
La fiabilité de cette mesure repose essentiellement sur la qualité de la prise de pression statique (point B) : la paroi doit être lisse et sans imperfection au voisinage de l'orifice (évitant ainsi une surévaluation ou sous-évaluation de la pression). Bien qu'extrêmement simple et rudimentaire, ce dispositif équipe notamment les avions modernes pour évaluer leur vitesse de vol.
Effet Venturi
Associé au principe de conservation du débit d'un écoulement en conduite, la conservation de la pression totale le long des lignes de courant (équation de Bernoulli) conduit naturellement à observer l'effet Venturi : un élargissement (rétrécissement) local de la conduite provoque localement une surpression (dépression).
Cet effet est à la base d'un dispositif simple permettant la mesure du débit d'un écoulement.
Exemple :
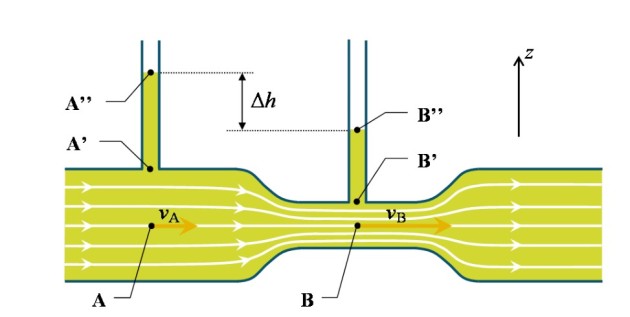
Il suffit d'aménager un rétrécissement le long d'une conduite cylindrique dans laquelle s'écoule un fluide supposé parfait et incompressible. Comme le montre le schéma de la figure 20, le fluide s'écoule à travers une section ![]() à la vitesse uniforme
à la vitesse uniforme ![]() avant d'atteindre le rétrécissement où la section
avant d'atteindre le rétrécissement où la section ![]() implique une vitesse
implique une vitesse ![]() . En effet, la conservation du débit volumique
. En effet, la conservation du débit volumique ![]() impose :
impose : ![]() , et donc
, et donc ![]() .
.
On peut ensuite appliquer l'équation de Bernoulli sur une ligne de courant passant par les deux points A et B :
La conduite étant horizontale, on a ![]() ; par ailleurs, on supposera que la pression est uniforme sur une même section : on a donc
; par ailleurs, on supposera que la pression est uniforme sur une même section : on a donc ![]() et
et ![]() , où A' et B' appartiennent aux mêmes sections que respectivement A et B, et sont situés à l'entrée de deux tubes manométriques. Par conséquent, la dénivellation lue
, où A' et B' appartiennent aux mêmes sections que respectivement A et B, et sont situés à l'entrée de deux tubes manométriques. Par conséquent, la dénivellation lue ![]() est une mesure de la différence de pression entre A' et B' :
est une mesure de la différence de pression entre A' et B' :
Donc : ![]() , et par ailleurs :
, et par ailleurs : ![]() . Par identification des deux résultats, on obtient :
. Par identification des deux résultats, on obtient :
On peut alors introduire le débit ![]() , pour exprimer :
, pour exprimer :
et obtenir une formulation du débit directement fonction de la dénivellation observée à l'aide des deux manomètres :
Il est évidemment possible d'en déduire les vitesses d'écoulement au niveau du rétrécissement et en amont :
Remarque :
Ce dispositif est couramment utilisé comme élément intégré aux circuits hydrauliques et permet une mesure simple du débit d'écoulement. Il génère toutefois des pertes de charge : c'est donc un dispositif de mesure qui dissipe de l'énergie. La perte de charge peut facilement être évaluée en plaçant en amont du rétrécissement un troisième tube manométrique. Compte tenu du principe de conservation du débit, à section égale, la vitesse y est la même que ![]() . L'application de l'équation de Bernoulli entre l'amont et l'aval impose donc d'avoir la même pression si le fluide est parfait (non visqueux). Or, une mesure réelle montre que la pression en aval est inférieure à celle en amont : cela signifie simplement que lorsque les frottements ne peuvent être négligés (viscosité non nulle) l'équation de Bernoulli établie pour un fluide parfait n'est pas valable ; le rétrécissement génère en pratique une chute de la pression totale que l'on qualifiera de perte de charge singulière (voir chapitre à venir sur les pertes de charge).
. L'application de l'équation de Bernoulli entre l'amont et l'aval impose donc d'avoir la même pression si le fluide est parfait (non visqueux). Or, une mesure réelle montre que la pression en aval est inférieure à celle en amont : cela signifie simplement que lorsque les frottements ne peuvent être négligés (viscosité non nulle) l'équation de Bernoulli établie pour un fluide parfait n'est pas valable ; le rétrécissement génère en pratique une chute de la pression totale que l'on qualifiera de perte de charge singulière (voir chapitre à venir sur les pertes de charge).
Vidange d'un réservoir - formule de Torricelli
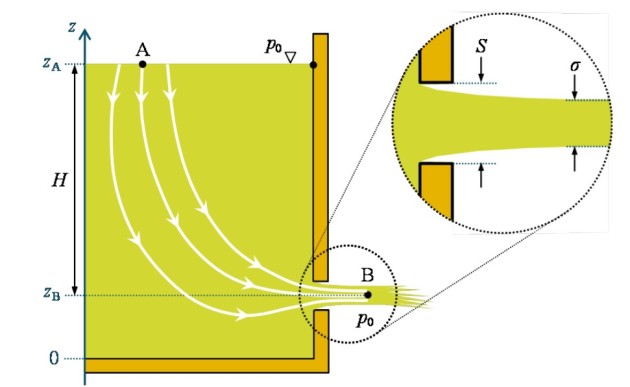
Considérons un réservoir de grande section, rempli d'un liquide qui s'écoule à travers un orifice de section faible (devant celle du réservoir) et situé à une hauteur ![]() sous la surface libre (voir figure 21). La pression atmosphérique s'exerce à la fois sur la surface libre et sur le jet à la sortie de l'orifice. En supposant que le liquide est incompressible et non visqueux, il est possible d'utiliser l'équation de Bernoulli pour déterminer la vitesse de vidange du réservoir.
sous la surface libre (voir figure 21). La pression atmosphérique s'exerce à la fois sur la surface libre et sur le jet à la sortie de l'orifice. En supposant que le liquide est incompressible et non visqueux, il est possible d'utiliser l'équation de Bernoulli pour déterminer la vitesse de vidange du réservoir.
Considérons un point A de la surface libre et un point B situé dans le jet. Il existe une ligne de courant passant par ces deux points et le long de laquelle on peut appliquer l'équation de Bernoulli :
Compte tenu du rapport de section entre le réservoir et l'orifice, on peut y négliger ![]() devant
devant ![]() . Par ailleurs, le point A étant situé sur la surface libre, on a :
. Par ailleurs, le point A étant situé sur la surface libre, on a : ![]() . Dans le domaine du jet où se trouve le point B, les lignes de courant sont rectilignes et parallèle et par conséquent la pression motrice
. Dans le domaine du jet où se trouve le point B, les lignes de courant sont rectilignes et parallèle et par conséquent la pression motrice ![]() est uniforme sur une même section. En négligeant les variations d'altitude au sein du jet, il s'ensuit que la pression statique est également à peu près uniforme sur une même section. Or, par continuité de la pression à l'interface jet-atmosphère, la pression atmosphérique règne donc en tout point du jet (ce résultat peut être généralisé à toute situation dans laquelle un liquide s'écoule sous la forme d'un jet libre).
est uniforme sur une même section. En négligeant les variations d'altitude au sein du jet, il s'ensuit que la pression statique est également à peu près uniforme sur une même section. Or, par continuité de la pression à l'interface jet-atmosphère, la pression atmosphérique règne donc en tout point du jet (ce résultat peut être généralisé à toute situation dans laquelle un liquide s'écoule sous la forme d'un jet libre).
Fondamental :
On en déduit donc que ![]() , et l'équation de Bernoulli prend la forme suivante :
, et l'équation de Bernoulli prend la forme suivante :
qui, après simplification, permet d'écrire la formule deTorricelli :
Remarque :
La vitesse d'écoulement du liquide est indépendante de sa masse volumique ; le seul paramètre dont dépend la vitesse de vidange est donc la hauteur de liquide séparant l'orifice de la surface libre.
L'évaluation du débit de vidange nécessite de prendre en compte la contraction du jet. Comme le montre l'encart de la figure 21, la vitesse évaluée précédemment correspond à une section plus faible que celle de l'orifice. En conséquence, le débit volumique de vidange s'obtient en calculant :
où ![]() est la section du jet où les lignes de courant peuvent être considérées rectilignes et parallèles. On peut ainsi définir un coefficient de contraction
est la section du jet où les lignes de courant peuvent être considérées rectilignes et parallèles. On peut ainsi définir un coefficient de contraction ![]() , lequel dépend essentiellement du type de paroi ainsi que du profil de l'orifice dans la paroi. On peut alors reformuler le débit de vidange ainsi :
, lequel dépend essentiellement du type de paroi ainsi que du profil de l'orifice dans la paroi. On peut alors reformuler le débit de vidange ainsi :
Exemple :
La figure 22 donne de manière non exhaustive quelques valeurs typiques de ce coefficient de contraction.
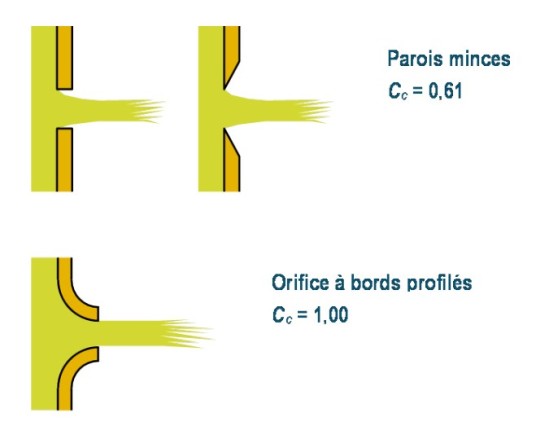
Phénomène de cavitation
Compte tenu de l'équation de Bernoulli, lorsqu'au sein d'un écoulement la vitesse atteint localement des valeurs élevées, la pression du liquide chute et peut tomber sous le seuil de pression de vapeur saturante. Dans ce cas, il y a localement transition de phase et vaporisation du liquide (voir figure 23). Les bulles de vapeur ainsi formées perturbent l'écoulement et nuisent généralement au bon fonctionnement des dispositifs dans lesquels elles apparaissent (pompes, hélices propulsives...). Notamment, la migration de ces bulles vers des régions de plus haute pression provoque leur implosion : le choc mécanique ainsi produit constitue un facteur d'endommagement prématuré des hélices.

Exemple :
A 20°C la pression de vapeur saturante de l'eau est de 2,34 kPa.
Remarque :
La cavitation peut également être générée par la propagation d'une onde acoustique (généralement des ultrasons de puissance) ; on parle alors plutôt de cavitation acoustique, par distinction avec la cavitation hydrodynamique décrite précédemment.