Définitions
Un écoulement est qualifié d'irrotationnel lorsque les particules fluides ne subissent pas de rotation pure, autrement dit quand le tenseur des rotations pures ![]() est nul (voir
est nul (voir « Dynamique des fluides »
A.3). Rappelons que ce tenseur antisymétrique est constitué des composantes du vecteur tourbillon ![]() et qu'en conséquence ce dernier doit être nul en tout point de l'écoulement :
et qu'en conséquence ce dernier doit être nul en tout point de l'écoulement :
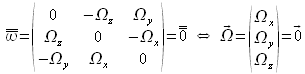
Puisque le vecteur tourbillon n'est autre que le rotationnel du vecteur vitesse ![]() , il en résulte qu'un écoulement irrotationnel doit vérifier :
, il en résulte qu'un écoulement irrotationnel doit vérifier :
Or, quelle que soit la fonction scalaire ![]() , la relation mathématique
, la relation mathématique ![]() est toujours vraie. Donc, par identification de
est toujours vraie. Donc, par identification de ![]() avec
avec ![]() , on peut définir le champ de vecteurs vitesse d'un écoulement à partir de la seule fonction scalaire
, on peut définir le champ de vecteurs vitesse d'un écoulement à partir de la seule fonction scalaire ![]() , que l'on nommera désormais potentiel des vitesses. Il en résulte que les composantes du vecteur vitesse s'expriment en fonction des dérivées partielles du potentiel des vitesses :
, que l'on nommera désormais potentiel des vitesses. Il en résulte que les composantes du vecteur vitesse s'expriment en fonction des dérivées partielles du potentiel des vitesses :
Sur la base des mêmes hypothèses que celles posées pour définir la fonction de courant, supposons que l'écoulement soit conservatif en plus d'être irrotationnel : dans ces conditions, on doit vérifier l'équation de continuité sous sa forme : ![]() ; ce qui conduit à :
; ce qui conduit à :
On en conclut que le potentiel des vitesses doit vérifier l'équation de Laplace.
Remarque :
Si l'écoulement est irrotationnel, la fonction de courant doit également vérifier l'équation de Laplace. En effet, on a :
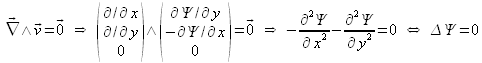
Propriétés du potentiel des vitesses
Au sein d'un écoulement plan, l'équation ![]() définit une courbe qu'on nommera
définit une courbe qu'on nommera « équipotentielle »
. Le potentiel des vitesses étant constant le long d'une telle courbe, on doit vérifier ![]() . Or,
. Or, ![]() et
et ![]() , d'où :
, d'où : ![]() devant être vérifiée en tout point de l'équipotentielle. Autrement formulé, on a :
devant être vérifiée en tout point de l'équipotentielle. Autrement formulé, on a :
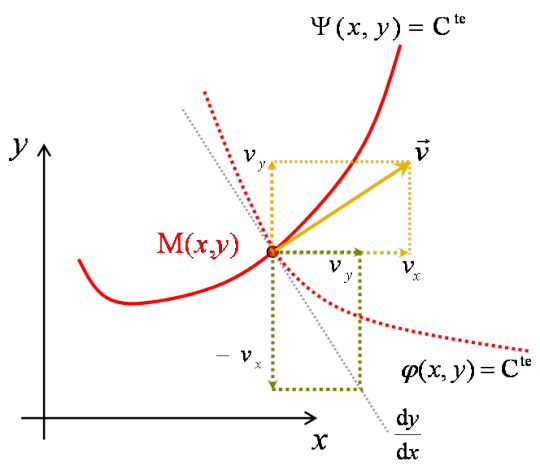
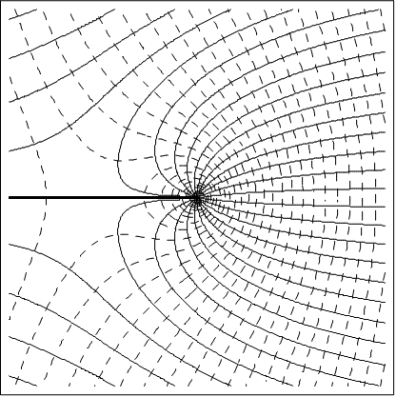
ce qui signifie qu'en chacun de ses points, la courbe est orthogonale au vecteur vitesse (voir figure 43). Il en résulte par ailleurs que les équipotentielles sont partout orthogonales aux lignes de courant. La figure 44 illustre cette propriété à partir d'un exemple d'écoulement plan où les lignes de courant sont représentées en traits pleins et les équipotentielles en traits pointillés.
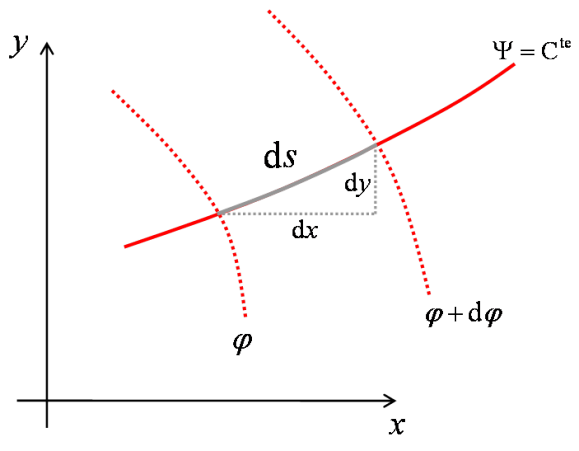
La signification physique de ces équipotentielles se comprend à travers le calcul de la longueur d'un élément d'arc le long d'une ligne de courant entre deux équipotentielles (voir figure 45). Si les deux équipotentielles sont infiniment proches, on peut considérer que leurs deux constantes respectives diffèrent d'une quantité élémentaire ![]() (l'une est de constante
(l'une est de constante ![]() , l'autre de constante
, l'autre de constante ![]() ). Si on note
). Si on note ![]() la longueur de l'élément d'arc, il peut se décomposer en
la longueur de l'élément d'arc, il peut se décomposer en ![]() .
.
Par ailleurs, on a déjà établi que ![]() , avec localement le long de la ligne de courant
, avec localement le long de la ligne de courant ![]() , d'où
, d'où ![]() et donc
et donc ![]() . On obtient de même
. On obtient de même ![]() , et on en déduit que :
, et on en déduit que : ![]() et
et ![]() . Ainsi, la longueur de l'élément d'arc se reformule :
. Ainsi, la longueur de l'élément d'arc se reformule :
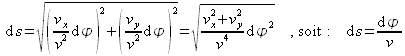
Ce résultat permet de statuer sur le fait que la distance entre deux équipotentielles est inversement proportionnelle à la vitesse locale de l'écoulement. L'exemple de la figure 44 illustre bien qu'en choisissant un écart ![]() constant entre les équipotentielles tracées, un resserrement de celles-ci traduit une accélération de l'écoulement, alors qu'à l'inverse un espacement traduit une décélération. On comprend alors l'intérêt de représenter, en plus des lignes de courant, les équipotentielles qui permettent d'avoir une vision complète de l'écoulement en terme d'évolution spatiale des vitesses.
constant entre les équipotentielles tracées, un resserrement de celles-ci traduit une accélération de l'écoulement, alors qu'à l'inverse un espacement traduit une décélération. On comprend alors l'intérêt de représenter, en plus des lignes de courant, les équipotentielles qui permettent d'avoir une vision complète de l'écoulement en terme d'évolution spatiale des vitesses.




