Définition de la fonction de courant
Considérons l'écoulement conservatif d'un fluide incompressible. Dans ce cas, l'équation de continuité se formule simplement par : ![]() . Par ailleurs, quelle que soit la quantité vectorielle
. Par ailleurs, quelle que soit la quantité vectorielle ![]() , en tout point de l'espace la relation mathématique
, en tout point de l'espace la relation mathématique ![]() doit être vérifiée. Donc, par identification, on peut définir en tout point de l'espace le vecteur vitesse comme résultant de
doit être vérifiée. Donc, par identification, on peut définir en tout point de l'espace le vecteur vitesse comme résultant de ![]() , où
, où ![]() peut alors être qualifié de
peut alors être qualifié de « potentiel vecteur »
. La connaissance de ce potentiel vecteur en tout point de l'espace permet donc d'en déduire les trois composantes du vecteur vitesse en ce même point :
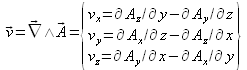
Considérons maintenant que l'écoulement est bidimensionnel, dans le plan ![]() , impliquant que
, impliquant que ![]() et qu'il y ait invariance par translation suivant
et qu'il y ait invariance par translation suivant ![]() , d'où
, d'où ![]() . Il reste alors :
. Il reste alors :
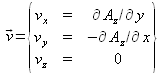
Dans ces conditions, on note que chaque vecteur vitesse est défini au moyen de seulement deux composantes et que celles-ci dérivent d'une seule composante parmi les trois du potentiel vecteur. On peut donc en conclure que le champ de vecteurs vitesse d'un écoulement plan dérive d'une quantité scalaire, la fonction de courant ![]() . La connaissance de cette seule fonction de courant permet alors d'en déduire le champ de vecteurs vitesse en tout point de l'écoulement, par simple application de :
. La connaissance de cette seule fonction de courant permet alors d'en déduire le champ de vecteurs vitesse en tout point de l'écoulement, par simple application de :
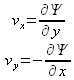
Remarque :
Dans un système de coordonnées cylindriques, la démarche reste la même et conduit à définir![]() pour exprimer les composantes cylindriques du vecteur vitesse comme :
pour exprimer les composantes cylindriques du vecteur vitesse comme :
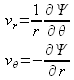
Propriétés de la fonction de courant
Partant de la fonction de courant pour définir le vecteur vitesse, l'équation de continuité appliquée dans le cadre d'un écoulement plan et conservatif d'un fluide incompressible permet d'établir une propriété remarquable de la fonction de courant :
d'où :
On en déduit par conséquent que ![]() est une différentielle totale exacte et que
est une différentielle totale exacte et que ![]() possède une seule et unique primitive. En pratique, lorsqu'on intègre
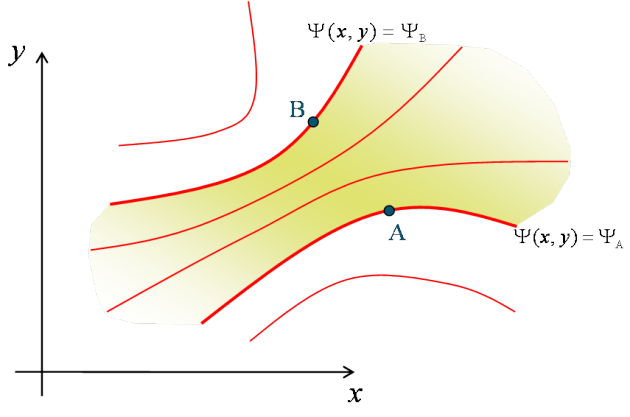
possède une seule et unique primitive. En pratique, lorsqu'on intègre ![]() d'un point A à un point B du plan, le résultat de l'intégration ne dépend donc pas du chemin suivi entre ces deux points :
d'un point A à un point B du plan, le résultat de l'intégration ne dépend donc pas du chemin suivi entre ces deux points :
Dans le plan de l'écoulement, l'ensemble des points pour lesquels la fonction de courant renvoie une valeur constante définit une courbe particulière : il s'agit d'une courbe le long de laquelle ![]() , où doit être vérifié :
, où doit être vérifié : ![]() . Or, puisque
. Or, puisque ![]() et
et ![]() , on peut écrire :
, on peut écrire : ![]() , ce qui signifie qu'en chaque point de cette courbe, doit être vérifié :
, ce qui signifie qu'en chaque point de cette courbe, doit être vérifié :
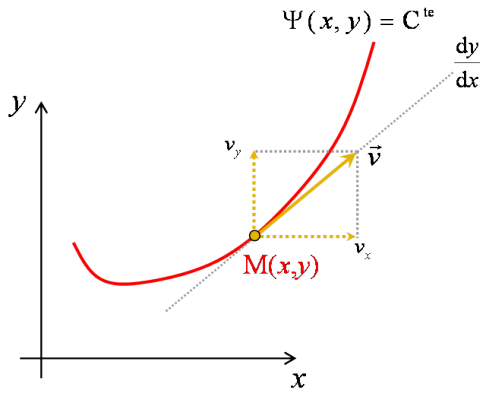
Autrement dit, la tangente à la courbe est en tout point identique à l'orientation du vecteur vitesse (voir figure 40). Une courbe qui présente cette propriété est alors une courbe que l'on a déjà définie comme étant une ligne de courant. Il en résulte que la fonction de courant est constante le long d'une ligne de courant.
Remarque :
A chaque ligne de courant correspond une constante différente comme valeur de la fonction de courant. On peut ainsi faire l'analogie avec les lignes de niveau des cartes topographiques : l'ensemble des lieux se trouvant à la même altitude constitue une courbe de niveau ; la fonction de courant est ainsi l'analogue de l'altitude. L'analogie peut être poussée en considérant que le passage d'une courbe de niveau à une autre induit une dénivellation qui est indépendante du chemin emprunté. Il en est de même pour la fonction de courant dont, on l'a vu, la différentielle est totale exacte.
Débit et lignes de courant
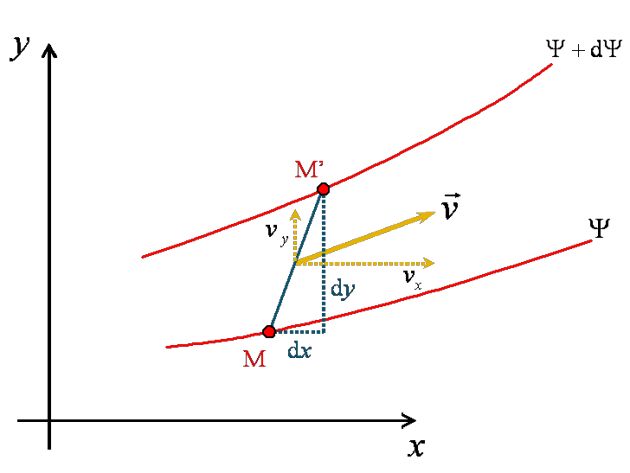
Considérons, au sein d'un écoulement plan, deux lignes de courant infiniment voisines (voir figure 41) et caractérisées par des fonctions de courant dont les constantes sont infiniment proches : ![]() et
et ![]() . Considérons par ailleurs deux points M et M' appartenant à chacune de ces deux lignes de courant et donnons nous pour objectif de calculer le débit volumique de l'écoulement à travers le segment [MM']. Il s'agit d'un débit élémentaire qui peut se décomposer en considérant la somme des débits traversant les projections selon
. Considérons par ailleurs deux points M et M' appartenant à chacune de ces deux lignes de courant et donnons nous pour objectif de calculer le débit volumique de l'écoulement à travers le segment [MM']. Il s'agit d'un débit élémentaire qui peut se décomposer en considérant la somme des débits traversant les projections selon ![]() et
et ![]() du segment MM'. On a ainsi :
du segment MM'. On a ainsi :
où le signe - rend compte du fait que le débit à travers ![]() contribue négativement au débit global. Or, les composantes de la vitesse peuvent se formuler en fonction des dérivées partielles de la fonction de courant :
contribue négativement au débit global. Or, les composantes de la vitesse peuvent se formuler en fonction des dérivées partielles de la fonction de courant :![]() et
et ![]() ; on obtient alors cette nouvelle formulation du débit élémentaire :
; on obtient alors cette nouvelle formulation du débit élémentaire :
On vient ainsi de montrer que ![]() .
.