Définition et contexte
Lorsqu'un écoulement plan est conservatif et irrotationnel, il peut être complètement décrit au moyen d'une fonction analytique complexe appelée « potentiel complexe des vitesses »
. Cette fonction complexe ![]() comporte une partie réelle correspondant au potentiel des vitesses
comporte une partie réelle correspondant au potentiel des vitesses ![]() et une partie imaginaire correspondant à la fonction de courant
et une partie imaginaire correspondant à la fonction de courant ![]() . On définit ainsi :
. On définit ainsi :
Remarque :
La définition d'une telle fonction analytique est légitime dans la mesure où le potentiel des vitesses et la fonction de courant vérifient les relations de Cauchy :![]() et
et ![]() .
.
L'intérêt de l'utilisation du potentiel complexe des vitesses est double :
il réunit en une seule fonction les deux fonctions descriptives de l'écoulement ;
il permet la construction d'écoulements évolués par simple superposition d'écoulements élémentaires :
Écoulement uniforme
Considérons l'écoulement plan dont le potentiel complexe des vitesses se formule :
où ![]() est une constante réelle.
est une constante réelle.
Par identification des parties réelle et imaginaire avec respectivement le potentiel des vitesses et la fonction de courant, on obtient :
Les lignes de courant sont alors définies par ![]() , d'où
, d'où ![]() : il s'agit donc de droites horizontales (toutes parallèles à l'axe
: il s'agit donc de droites horizontales (toutes parallèles à l'axe![]() ). Tandis que les équipotentielles sont définies par
). Tandis que les équipotentielles sont définies par ![]() , d'où
, d'où ![]() : il s'agit alors de droites verticales (toutes parallèles à l'axe
: il s'agit alors de droites verticales (toutes parallèles à l'axe ![]() ). Comme il se doit, on remarque que les lignes de courant sont de fait orthogonales aux équipotentielles.
). Comme il se doit, on remarque que les lignes de courant sont de fait orthogonales aux équipotentielles.
On peut par ailleurs en déduire le champ de vecteurs vitesse en utilisant soit la fonction de courant, soit le potentiel des vitesses :
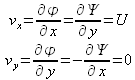
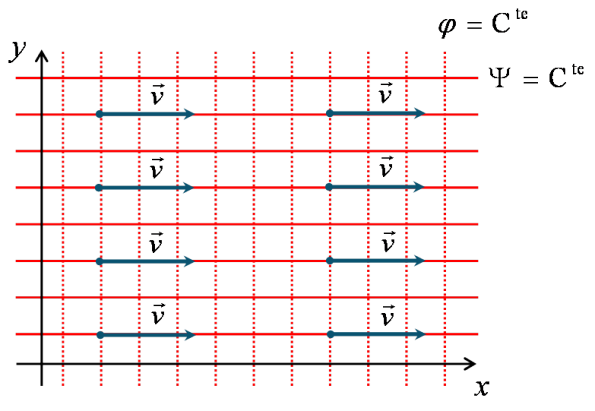
d'où ![]() en tout point de l'écoulement, correspondant à un écoulement uniforme de vitesse
en tout point de l'écoulement, correspondant à un écoulement uniforme de vitesse ![]() selon l'axe
selon l'axe ![]() , comme le montre la figure 46.
, comme le montre la figure 46.
Remarque :
L'utilisation d'une constante![]() complexe permet d'orienter l'écoulement uniforme selon une direction quelconque.
complexe permet d'orienter l'écoulement uniforme selon une direction quelconque.
Écoulement plan autour d'une source ou d'un puits
Considérons l'écoulement plan dont le potentiel complexe des vitesses se formule :
où ![]() est une constante réelle.
est une constante réelle.
Pour faciliter le traitement mathématique, il conviendra de travailler préférentiellement en coordonnées cylindriques ; ainsi :![]() et
et ![]() , où l'on peut identifier le potentiel des vitesses (partie réelle) et la fonction de courant (partie imaginaire) :
, où l'on peut identifier le potentiel des vitesses (partie réelle) et la fonction de courant (partie imaginaire) :
Les lignes de courant sont telles que ![]() , autrement dit il s'agit de droites passant toutes par l'origine du repère. Les équipotentielles doivent vérifier que
, autrement dit il s'agit de droites passant toutes par l'origine du repère. Les équipotentielles doivent vérifier que ![]() : il s'agit de cercles tous centrés sur l'origine du repère. On vérifie bien ainsi qu'en tout point de l'écoulement les équipotentielles sont orthogonales aux lignes de courant. Par ailleurs, le champ de vecteurs vitesse s'obtient en calculant :
: il s'agit de cercles tous centrés sur l'origine du repère. On vérifie bien ainsi qu'en tout point de l'écoulement les équipotentielles sont orthogonales aux lignes de courant. Par ailleurs, le champ de vecteurs vitesse s'obtient en calculant :
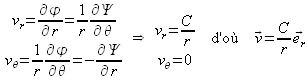
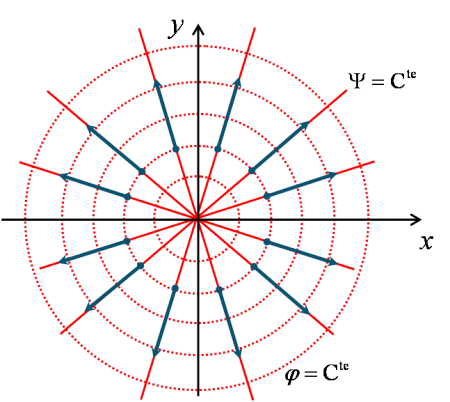
On a donc un écoulement radial, centré sur l'origine du repère, où la vitesse est inversement proportionnelle à la distance à l'origine (voir figure 47). On remarquera que selon le signe de la constante ![]() , l'écoulement peut être divergent ou convergent : si
, l'écoulement peut être divergent ou convergent : si ![]() alors l'écoulement est divergent et correspond à l'effet d'une source à l'origine ; si
alors l'écoulement est divergent et correspond à l'effet d'une source à l'origine ; si ![]() , l'écoulement est convergent et correspond à l'effet d'un puits à l'origine.
, l'écoulement est convergent et correspond à l'effet d'un puits à l'origine.
La signification physique de la constante ![]() est en rapport avec le débit généré par cette source ou ce puits. Pour s'en rendre compte, calculons le débit volumique de l'écoulement radial à travers un cylindre d'axe
est en rapport avec le débit généré par cette source ou ce puits. Pour s'en rendre compte, calculons le débit volumique de l'écoulement radial à travers un cylindre d'axe ![]() (perpendiculaire au plan de l'écoulement), de rayon
(perpendiculaire au plan de l'écoulement), de rayon ![]() , et de hauteur
, et de hauteur ![]() . L'écoulement ayant lieu à travers la surface latérale du cylindre, on peut calculer :
. L'écoulement ayant lieu à travers la surface latérale du cylindre, on peut calculer :
où ![]() et
et ![]() .
.
On obtient donc :
Ainsi, indépendamment du cylindre choisi, la constante ![]() est égale, à
est égale, à ![]() près, au débit généré par la source ou le puits. C'est la raison pour laquelle on formule communément l'écoulement généré par un puits (
près, au débit généré par la source ou le puits. C'est la raison pour laquelle on formule communément l'écoulement généré par un puits (![]() ) ou une source (
) ou une source (![]() ) par :
) par :
où ![]() est le débit volumique par unité de hauteur de l'écoulement plan (en
est le débit volumique par unité de hauteur de l'écoulement plan (en ![]() ).
).
Remarque :
Cette formulation vaut pour un puits ou une source centré à l'origine du repère. On peut très bien envisager un écoulement centré en un point quelconque du plan, de coordonnées ![]() , en formulant simplement
, en formulant simplement ![]() .
.
Vortex ou tourbillon libre
Considérons l'écoulement plan dont le potentiel complexe des vitesses se formule :
où ![]() est une constante réelle.
est une constante réelle.
Une nouvelle fois, il est plus approprié de travailler dans un système de coordonnées cylindriques.
Développons cette fonction pour identifier le potentiel des vitesses et la fonction de courant :
d'où :
Les lignes de courant sont telles que ![]() , autrement dit il s'agit de cercles tous centrés sur l'origine du repère. Les équipotentielles doivent vérifier que
, autrement dit il s'agit de cercles tous centrés sur l'origine du repère. Les équipotentielles doivent vérifier que ![]() : il s'agit de droites passant toutes par l'origine du repère. On vérifie encore qu'en tout point de l'écoulement les équipotentielles sont orthogonales aux lignes de courant. Par ailleurs, le champ de vecteurs vitesse s'obtient en calculant :
: il s'agit de droites passant toutes par l'origine du repère. On vérifie encore qu'en tout point de l'écoulement les équipotentielles sont orthogonales aux lignes de courant. Par ailleurs, le champ de vecteurs vitesse s'obtient en calculant :
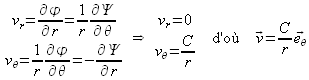
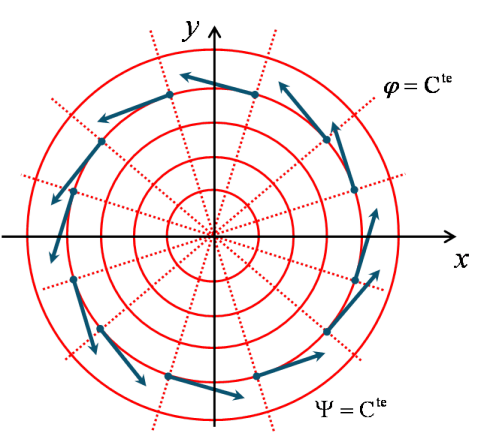
On a donc un écoulement orthoradial, tournant autour de l'origine du repère, où la vitesse est inversement proportionnelle à la distance à l'origine (voir figure 48). On notera la différence avec l'écoulement radial généré par un puits ou une source : les lignes de courant et les équipotentielles sont inter-changées. Par ailleurs, le signe de la constante ![]() définit le sens de rotation : si
définit le sens de rotation : si ![]() le vortex tourne dans le sens trigonométrique ; si
le vortex tourne dans le sens trigonométrique ; si ![]() , il tourne dans le sens horaire.
, il tourne dans le sens horaire.
La signification physique de la constante ![]() est en rapport avec la circulation du vecteur vitesse autour de l'origine du vortex. Pour le comprendre, calculons la circulation du vecteur vitesse le long d'une ligne de courant définie par un cercle de rayon
est en rapport avec la circulation du vecteur vitesse autour de l'origine du vortex. Pour le comprendre, calculons la circulation du vecteur vitesse le long d'une ligne de courant définie par un cercle de rayon ![]() centré sur l'origine ; on a ainsi :
centré sur l'origine ; on a ainsi :
On en déduit que la circulation est une propriété intrinsèque du vortex. En conséquence, on formulera plus communément le potentiel complexe des vitesses correspondant à un vortex en faisant apparaître sa circulation :
où ![]() le fait tourner dans le sens trigonométrique et
le fait tourner dans le sens trigonométrique et ![]() dans le sens horaire.
dans le sens horaire.
Remarque :
Cette formulation vaut pour un vortex tournant autour de l'origine du repère. On peut très bien envisager un vortex tournant autour d'un point quelconque du plan, de coordonnées ![]() , en formulant simplement
, en formulant simplement ![]() .
.
Doublet et dipôle
Considérons l'association d'un puits et d'une source au sein d'un même écoulement plan. Positionnons la source de débit ![]() en
en ![]() et le puits de débit
et le puits de débit ![]() en
en ![]() . Il s'agit alors de l'écoulement généré par un
. Il s'agit alors de l'écoulement généré par un « doublet »
. Puisque la superposition d'écoulements élémentaires s'opère par simple addition de leurs potentiels complexes des vitesses, l'association du puits et de la source se formule par :
Le traitement mathématique de cette fonction est simplifié en faisant appel à deux systèmes de coordonnées ; définissons alors deux repères cylindriques tels que :
et reformulons ![]() en conséquence :
en conséquence :
Par identification de la partie réelle avec le potentiel des vitesses et de la partie imaginaire avec la fonction de courant, on obtient :
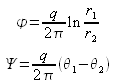
Par définition, les lignes de courant sont telles que ![]() et conduisent à tracer des courbes vérifiant :
et conduisent à tracer des courbes vérifiant : ![]() . La figure 49 montre alors que de telles courbes sont des cercles passant par l'origine du puits et l'origine de la source et ayant comme centre un point de l'axe
. La figure 49 montre alors que de telles courbes sont des cercles passant par l'origine du puits et l'origine de la source et ayant comme centre un point de l'axe ![]() . Sans faire le calcul du champ de vecteurs vitesse, on oriente intuitivement le parcours des particules fluides en constatant logiquement que l'écoulement diverge depuis la source et converge vers le puits.
. Sans faire le calcul du champ de vecteurs vitesse, on oriente intuitivement le parcours des particules fluides en constatant logiquement que l'écoulement diverge depuis la source et converge vers le puits.
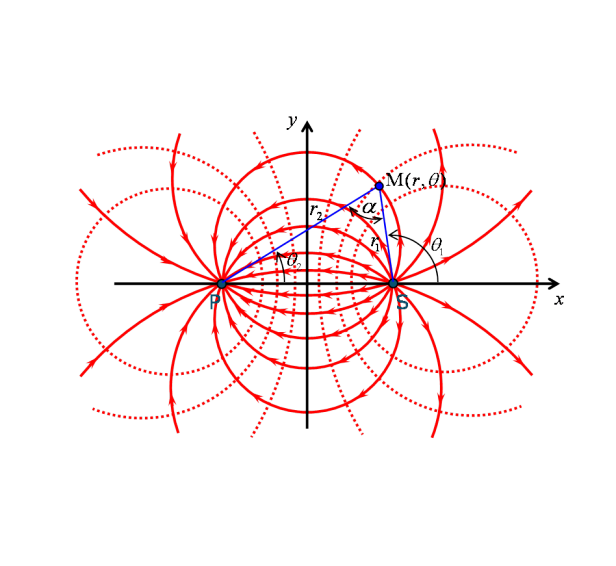
Remarque :
Intervertir les positions de la source et du puits ne change que le sens de parcours des particules le long des lignes de courant, ces dernières restant inchangées. Par ailleurs, les équipotentielles étant orthogonales en tout point aux lignes de courant, on comprend graphiquement (voir figure 49) qu'elles prennent la forme de cercles centrés sur l'axe ![]() .
.
Faisons tendre à présent vers zéro la distance entre le puits et la source : ![]() . Dans ces conditions, on superpose le puits et la source à l'origine, en créant ainsi un
. Dans ces conditions, on superpose le puits et la source à l'origine, en créant ainsi un « dipôle »
. Il convient alors de reformuler la fonction complexe dans un système de coordonnées unique :
et comme ![]() au premier ordre, on approxime :
au premier ordre, on approxime :
Posons alors ![]() le moment dipolaire caractérisant ce dipôle. Il en résulte la formulation suivante pour le dipôle :
le moment dipolaire caractérisant ce dipôle. Il en résulte la formulation suivante pour le dipôle :
où ![]() est une constante, qui peut être considérée complexe et permettre ainsi d'orienter à loisir le dipôle dans le plan de l'écoulement.
est une constante, qui peut être considérée complexe et permettre ainsi d'orienter à loisir le dipôle dans le plan de l'écoulement.
Faisons l'hypothèse d'un moment dipolaire réel positif et étudions l'écoulement qui en résulte. Il convient logiquement de travailler une fois encore dans un repère cylindrique et de développer ![]() pour identifier la fonction de courant et le potentiel des vitesses :
pour identifier la fonction de courant et le potentiel des vitesses :
d'où :
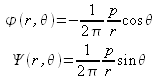
Une ligne de courant devant vérifier ![]() , son équation se formule :
, son équation se formule : ![]() . Montrons alors qu'il s'agit de l'équation d'un cercle :
. Montrons alors qu'il s'agit de l'équation d'un cercle :
Appelons ![]() la constante et poursuivons :
la constante et poursuivons :
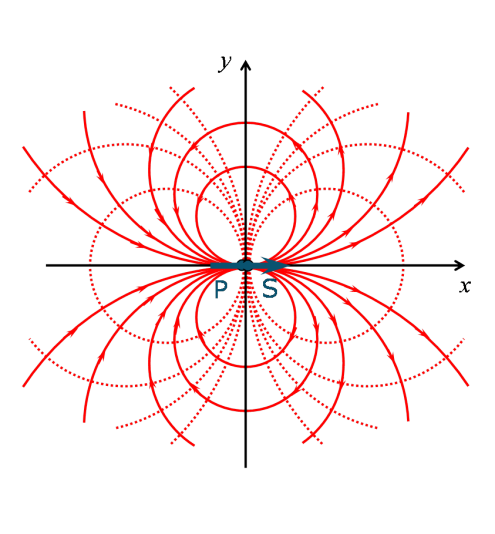
où l'on reconnaît l'équation d'un cercle de rayon ![]() et de centre se trouvant à
et de centre se trouvant à ![]() sur l'axe
sur l'axe ![]() . Ainsi, à chaque valeur différente de
. Ainsi, à chaque valeur différente de ![]() correspond une ligne de courant prenant la forme d'un cercle passant par l'origine et dont le centre se trouve sur l'axe
correspond une ligne de courant prenant la forme d'un cercle passant par l'origine et dont le centre se trouve sur l'axe ![]() (voir figure 50). On remarquera que, logiquement, les équipotentielles sont aussi des cercles passant par l'origine mais dont les centres se trouvent sur l'axe
(voir figure 50). On remarquera que, logiquement, les équipotentielles sont aussi des cercles passant par l'origine mais dont les centres se trouvent sur l'axe ![]() .
.
Remarque :
Les écoulements élémentaires présentés ici peuvent ensuite être associés pour former des écoulements plus évolués et susceptibles de décrire des situations concrètes. L'exemple le plus typique étant la superposition d'un écoulement uniforme avec un dipôle qui conduit à la description d'un écoulement autour d'un cylindre. Ce même cylindre peut ensuite être considéré en rotation autour de son axe en introduisant un vortex : l'analyse des vitesses au contact de la paroi du cylindre montre alors que la répartition des pressions (par simple application l'équation de Bernoulli) est à l'origine d'une force qui s'exerce perpendiculairement à la direction de l'écoulement uniforme. Il s'agit de la portance générée par l'effet Magnus.




