Définition :
La définition classique de l'impulsion
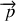d'une particule de masse
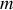est
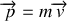. En faisant l'hypothèse que la masse
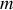d'une particule est un scalaire (Dans des textes plus anciens, il est parfois question de la masse relativiste
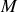, c'est-à-dire de la variation de
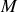avec la vitesse de la particule. Dans ce cas, il faut comprendre que
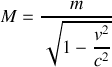), on a une généralisation évidente de la notion d'impulsion dans l'espace-temps à 4 dimensions :
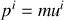
où les composantes du quadrivecteur vitesse
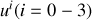sont données par les relations :
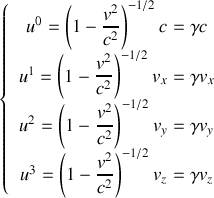
Ces composantes se transforment comme les coordonnées espace-temps d'un évènement (transformations de Lorentz). Les composantes spatiales de ce quadrivecteur se réduisent bien à l'impulsion classique à la limite
.
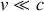Fondamental :
Qu'en est-il de la composante
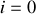du quadrivecteur impulsion ? La composante
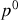s'écrit :
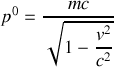
Considérons ensuite la grandeur
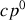que l'on développe en série, à la limite
:
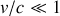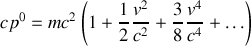
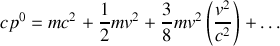
Le premier terme
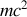est une constante, le second terme
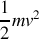est exactement l'énergie cinétique classique, et le troisième terme (ainsi que les suivants) peut-être regardé comme une correction relativiste à l'énergie cinétique. Comme l'énergie d'un système est définie classiquement à une constante arbitraire près, on identifie donc la grandeur
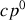à l'énergie
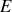de la particule.
Ces relations permettent d'obtenir la formule la plus célèbre d'Einstein. En relativité, on attribue une quantité d'énergie intrinsèque à une particule au repos, elle est proportionnelle à sa masse :
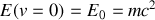
Cette formule est à la base de toute la physique nucléaire et de la physique des hautes énergies. Ainsi elle nous indique que si on concentre en un point de l'espace une quantité d'énergie équivalente à la masse d'une particule, celle-ci peut se matérialiser. Notons que dans certains livres, on exprimera l'énergie totale
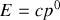en fonction de la masse relativiste
:
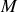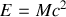
Définition :
La pseudo-norme du quadrivecteur impulsion
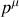vaut :
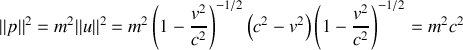
Fondamental :
comme
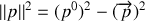
il vient
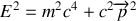
Il s'agit de la relation relativiste entre énergie et impulsion.
Remarque :
A la limite non relativiste, cette relation s'écrit :
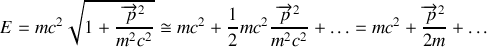
Le premier terme est l'énergie de la particule au repos, et le second terme représente l'énergie cinétique bien connue. Les termes négligés sont des corrections relativistes d'ordre supérieur.
Remarque :
Pour des particules de masse nulle
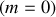, la relation entre énergie et impulsion se réduit à :
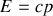
Pour éviter des problèmes de consistance dans la définition de l'impulsion, il faut compenser l'annulation du numérateur par celle du dénominateur, dans l'expression de
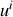. En conséquence de quoi, les particules de masse nulle se meuvent nécessairement à la vitesse de la lumière
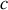(exemple : les photons).
