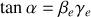Lié au mouvement de la Terre autour du Soleil (et approché par une translation), ce phénomène a été mis pour la première fois en évidence, dans un cadre non relativiste, par J. Bradley en 1728 (voir figure). Observant une étoile située sur un axe perpendiculaire au plan de l'écliptique, les photons reçus sur Terre semblaient émis par une source lumineuse décrivant au cours de l'année un cercle dont le diamètre apparent vaut
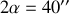 .
.
Exemple :
Quelle est l'expression analytique de
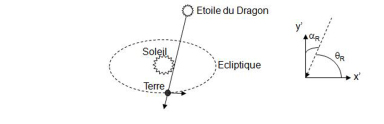
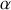 ? L'écliptique est le référentiel fixe
? L'écliptique est le référentiel fixe
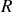 et la Terre est le référentiel en mouvement
et la Terre est le référentiel en mouvement
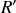 .
.
La transformation de Lorentz appliquée à la composante
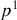 du quadrivecteur
du quadrivecteur
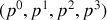 s'écrit :
s'écrit :
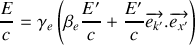
Tenant compte de l'effet Doppler-Fizeau, on obtient :
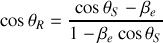
De même, la transformation de Lorentz s'applique à la composante
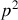 :
:
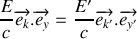
soit
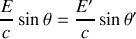
On obtient, à l'aide de l'équation de l'effet Doppler-Fizeau la relation :
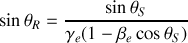
Considérons les équations angulaires. Lorsque
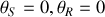 . Par contre, lorsque
. Par contre, lorsque
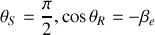 et
et
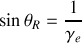 soit
soit
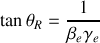 Comme
Comme
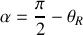 ,
,