Définition :
L'effet Doppler-Fizeau est la variation de la fréquence d'un signal lumineux lorsque la source et le récepteur sont en mouvement relatif
Considérons deux référentiels d'inertie
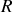et
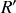, le premier lié à la source
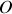et le second lié au récepteur
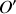. La source émet une onde lumineuse plane monochromatique de fréquence
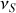dans la direction du vecteur d'onde
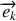(voir figure).
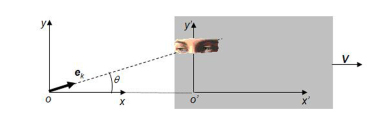
La source émet une onde lumineuse plane monochromatique de fréquence
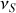dans la direction de
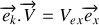est la vitesse d'éloignement du récepteur par rapport à la source.
Fondamental :
Suivant que le signal est reçu dans la direction de la vitesse
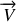ou dans une direction normale à
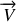, l'effet Doppler-Fizeau est qualifié de longitudinal ou de transversal. Le problème posé est le calcul de la fréquence
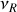détectée dans
.
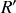La relation
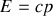donnant la norme (spatiale) du vecteur impulsion, le quadrivecteur énergie-impulsion du photon émis en
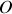s'écrit :
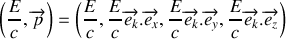
La transformation de Lorentz, appliquée à la composante
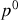du quadrivecteur
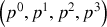s'écrit :
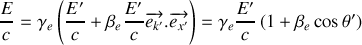
L'énergie d'un photon s'exprime en fonction de sa fréquence par la relation
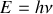où
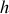est la constante de Planck. En développant l'équation ci-dessus, on obtient :
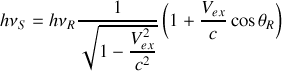
i) Effet Doppler-Fizeau longitudinal :
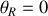, donc
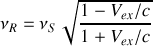
Cette équation indique que si le récepteur s'éloigne de la source
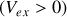, la fréquence reçue est plus petite que la fréquence émise. Par contre si le récepteur s'approche de la source
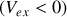, la fréquence reçue est plus grande que la fréquence émise. En terme de longueurs d'onde, on utilise la relation
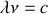. Cet effet est utilisé en astrophysique pour déterminer la vitesse des étoiles et des galaxies. A la limite non-relativiste
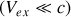, on obtient une formulation approchée :
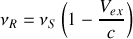
C'est la formule classique de l'effet Doppler.
ii) Effet Doppler-Fizeau transversal :
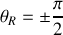, donc
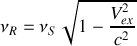
Cet effet est purement relativiste puisqu'en mécanique newtonienne (
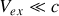), au premier ordre,
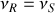. Il est très faible par rapport à l'effet Doppler-Fizeau longitudinal.
