Définition :
Noté
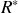, le référentiel du centre de masse est le référentiel en translation par rapport au référentiel
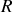du laboratoire, tel que la quantité de mouvement totale du système est nulle :
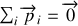
Fondamental :
Pour déterminer la vitesse d'entraînement
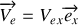de
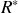par rapport à
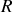, appliquons la transformation de Lorentz aux composante
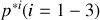du quadrivecteur impulsion-énergie :
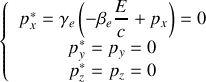
On obtient immédiatement la condition :
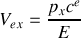
Application : collision élastique dans le référentiel
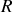d'une particule
(le « projectile »), animée d'une vitesse
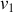, avec une particule
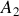(la « cible ») au repos. Dans
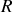, la conservation de l'impulsion et de l'énergie s'écrivent :
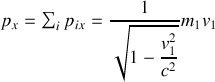
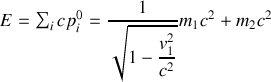
En insérant ces deux dernières équations dans celle qui précède, on obtient :
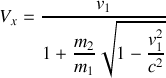
Quel est l'intérêt de travailler dans
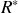? Lorsque la collision est élastique, on peut montrer que chaque particule conserve son énergie et la norme de sa quantité de mouvement :
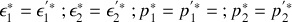
ce qui permet à l'aide de mesures de savoir, par exemple, très simplement si la collision étudiée est élastique ou non. On peut également obtenir des expressions analytiques donnant les angles de diffusion des deux particules après la collision.
