De la même façon que nous avons défini dans l'étude de l'électrostatique dans les milieux matériels une densité de dipôles, dans le cas du magnétisme on définit à partir du moment local une densité d'aimantation volumique
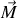telle que
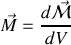
S'il y a des excédents locaux de courant liés à cette aimantation, il apparaît donc, encore une fois par analogie avec les relations établies en électrostatique pour la densité de charges, un courant d'aimantation volumique
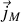tel que
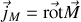
Remarque :
Si l'aimantation est uniforme, ces courants sont nuls, sauf éventuellement près de la surface où il y aura forcément une discontinuité de
.
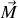On définit ainsi une densité de courants d'aimantation de surface dirigée vers l'extérieur du matériau :
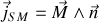
comme nous avions défini la densité de charges surfaciques d'un matériau.
Exemple :
Dans le cas d'un aimant cylindrique magnétisé uniformément suivant son axe avec
.
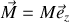Il apparaît une densité de courants d'aimantation orthoradiale
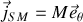, et ce système est donc totalement analogue à un solénoïde à
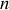spires par unité de longueur parcouru par un courant surfacique
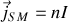, ce qui nous permet de calculer facilement le champ magnétique créé sur l'axe :
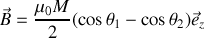
où
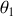et
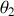sont les angles sous lesquels les faces sont vues.
