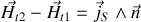De la même façon que nous avions modifié l'équation de Maxwell-Gauss pour prendre en compte l'effet sur le champ électrique de toutes les charges (libres et liées au milieu) et ainsi introduit le vecteur déplacement électrique, il nous faut désormais modifier l'équation de Maxwell-Ampère de la même façon.
Le champ magnétique
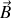est toujours de divergence nulle, mais ses sources consistent en tous les courants (libres de densité
, de déplacement
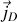et liés au matériau : courants d'aimantation
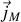et de polarisation
).
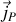Ainsi l'équation de Maxwell-Ampère s'écrit-elle :
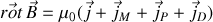
ou en remplaçant ces divers courants par leurs expressions :
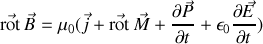
souvenons-nous que le vecteur déplacement électrique
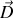est défini par :
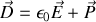
il vient donc :
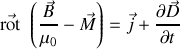
et si nous définissons un vecteur excitation magnétique
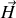tel que :
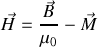
il vient :
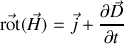
forme modifiée des équations de Maxwell-Ampère dans un milieu matériel.
Remarque :
Si nous prenons la divergence de cette expression, en vertu de la loi de conservation de la charge il apparaît :
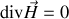
Dans un régime quasi-permanent, le terme dépendant du temps disparaît et on obtient le théorème d'Ampère dans un milieu matériel parcouru par un courant
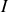traversant une surface enserrée par un circuit
:
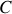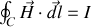
Complément :
De même on peut démontrer que les relations de passage entre deux milieux (théorème de Coulomb) sont analogues à celles obtenues pour
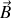au facteur
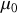près : la composante tangentielle de
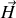entre deux milieux varie de :
