Considérons le modèle d'un électron dans l'atome de Bohr. Si on fait passer progressivement de
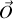à
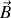la valeur du champ magnétique appliqué, le mouvement de l'électron se trouve perturbé.
Cette perturbation, action d'un champ magnétique sur le courant constitué par la circulation de l'électron autour du noyau, est donc un phénomène d'induction et obéit à la loi de Lenz, en sens opposé à la perturbation : d'où la création d'un moment magnétique en sens contraire à
.
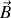Le diamagnétisme est une propriété générale qui peut être cachée par des propriétés supplémentaires du matériau (paramagnétisme, ferromagnétisme).
En l'absence de champ magnétique (pour t<0 par exemple) supposons que la vitesse angulaire de l'électron vaut
.
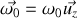La force
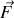qui s'exerce sur l'électron se réduit à la force électrostatique de Coulomb proportionnelle au champ électrique
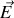et vaut
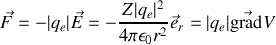
avec
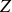le nombre de protons dans le noyau,
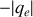la charge de l'électron,
sa distance au noyau ,
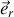le vecteur radial et
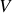le potentiel créé par le noyau.
Si l'on applique progressivement
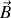entre les instants
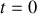et
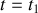(avec
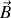constant pour
) une nouvelle force
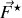apparaît et s'exerce sur l'électron de vitesse
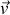: c'est une combinaison de la force de Lorentz et de l'effet du champ de Neumann
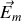
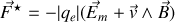
avec
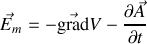
où
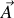est le potentiel vecteur dont dérive
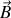(voir les chapitres précédents).
Si
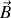est constant dans l'espace (c'est sûrement vrai pour un champ extérieur à l'échelle de l'atome) on peut prendre
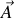suivant
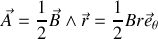
si nous supposons de plus que
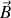est suivant la direction
.
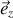Finalement comme le terme de Lorentz
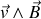est donc suivant
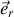car
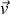reste suivant
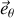tant que la perturbation due au champ n'est pas trop importante, on peut décomposer
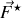en deux contributions suivant
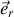et suivant
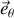
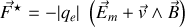
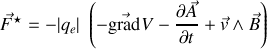
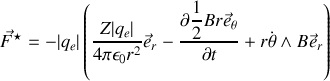
or en écrivant le principe fondamental de la dynamique pour l'électron dans un référentiel supposé galiléen
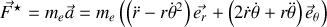
en notant
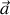l'accélération de l'électron de masse
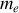supposé rester dans le plan de son orbite de départ
.
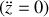Remarque :
Si nous supposons que l'effet du champ magnétique se réduit à perturber la vitesse angulaire de l'électron et non sa distance au proton r on peut négliger les termes \dot{r} et il vient donc en égalant les composantes des forces sur
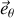
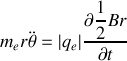
or
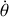est égal à la vitesse angulaire de l'électron
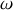donc après simplification par
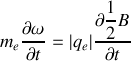
et après intégration temporelle
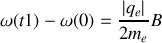
La vitesse angulaire aura donc varié d'une quantité
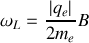appelée pulsation de Larmor, qui vaut la moitié de la pulsation cyclotron de l'électron.
On arriverait au même résultat en étudiant la composante
.
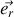On peut également voir l'effet du champ magnétique comme le passage à un référentiel tournant, précessant justement à cette vitesse angulaire
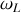(théorème de Larmor).
Une solution complète du problème montrerait que
varie de
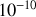en valeur relative pour des valeurs usuelles de champ magnétique et donc que l'approximation
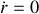est parfaitement justifiée.
On peut également arriver à ce résultat par le théorème du moment cinétique dans le référentiel supposé galiléen.
Si nous reprenons les notations du début du chapitre le moment des forces magnétiques est donc tel que
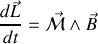
avec
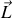moment cinétique de l'électron,
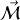moment magnétique.
En reprenant la définition du facteur de Landé
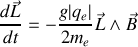
Par conséquent
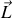est constant (puisque sa variation lui est orthogonale) et en se souvenant des formules de transformation des vecteurs dans un référentiel en rotation
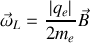on retrouve bien tous les phénomènes expliqués quelques paragraphes plus haut (précession de Larmor). Le lecteur conviendra que cette méthode est très rapide et très efficace, avec le facteur de Landé en plus, mais le phénomène est moins visible qu'avec une approche explicite.
Attention :
Le phénomène est largement utilisé expérimentalement pour étudier les propriétés de la matière : résonance électronique, résonance magnétique nucléaire, etc, en utilisant deux champs magnétiques orthogonaux, l'un fixe et très important et l'autre variable pour sonder la variation de fréquence de résonance du système.
