Pour résumer le paragraphe précédent, l'effet d'un champ magnétique extérieur
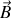 appliqué à un atome de Bohr est de faire varier la vitesse angulaire
appliqué à un atome de Bohr est de faire varier la vitesse angulaire
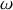 de l'électron d'une quantité
de l'électron d'une quantité
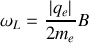 .
.
Si nous revenons au calcul de l'intensité du courant créé par la rotation de l'électron autour du noyau cette vitesse angulaire supplémentaire correspond à une intensité électrique supplémentaire
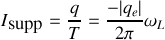
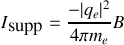
et le moment magnétique de l'électron est donc affecté d'une quantité supplémentaire
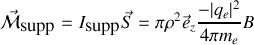
avec
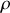 rayon de la projection de l'orbite de Bohr sur le plan
rayon de la projection de l'orbite de Bohr sur le plan
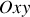 orthogonal à la direction du champ magnétique
orthogonal à la direction du champ magnétique
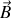 .
.
En moyenne sur une assemblée d'atomes cette valeur
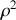 se moyenne à la somme des moyennes de
se moyenne à la somme des moyennes de
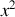 et de
et de
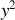 , c'est à dire à 2/3 de la moyenne de
, c'est à dire à 2/3 de la moyenne de
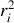 rayon de l'orbite de Bohr du i-ème électron.
rayon de l'orbite de Bohr du i-ème électron.
Ainsi pour une assemblée d'atomes indépendants la moyenne de la variation de moment magnétique par électron vaudra
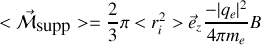 .
.
Si chaque atome possède
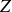 électrons indépendants la résultante vaut
électrons indépendants la résultante vaut
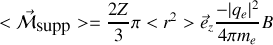
En supposant qu'il y a
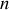 atomes par unité de volume l'aimantation supplémentaire vaut
atomes par unité de volume l'aimantation supplémentaire vaut
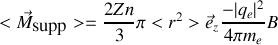
or par définition
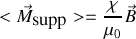
donc la susceptibilité diamagnétique
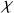 vaut dans ces approximations
vaut dans ces approximations
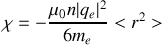
Remarque :
Cette susceptibilité est bien négative comme nous l'avions prévu à partir de la loi de Lenz, et que sa valeur est très faible. Une application numérique pour un gaz tel que l'hydrogène atomique donne ainsi
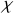 proche de
proche de
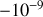 et pour un liquide ou pour un solide
et pour un liquide ou pour un solide
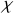 proche de
proche de
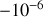 .
.



