L'aimantation résultante 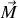est somme des contributions des dipôles individuels, qui auront évidemment tendance à s'aligner de façon parallèle au champ magnétique, les autres composantes se moyennant à zéro par symétrie de l'agitation thermique. Il suffit donc de calculer la composante de 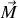suivant

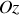
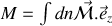
avec 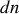le nombre de dipôles dans l'angle solide ,

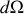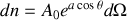
La constante de proportionnalité 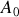étant donnée par la condition de normalisation sur le nombre total 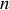de dipôles dans la région considérée

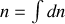
soit

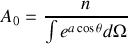
Finalement

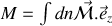
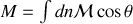
or en coordonnées sphériques, l'élément de surface 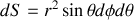d'une sphère vaut 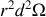donc après intégration sur l'angle 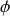(rotation autour de la direction du champ magnétique n'ayant pas d'influence géométrique sur le résultat) il vient :

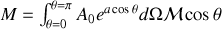
comme :

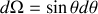
on a :

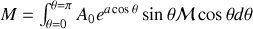
en substituant la valeur de

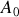
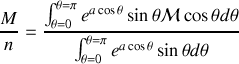
soit encore

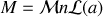
avec 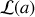fonction de Langevin que nous avons déjà rencontrée dans le chapitre précédent sur l'électrostatique dans les milieux matériels, ce qui n'est pas très étonnant vu la similitude des phénomènes.

En reconnaissant cette fonction comme une dérivée logarithmique de son dénominateur rappelons qu'il vient :

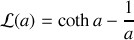
Aux faibles températures (pour 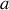grand) cette fonction tend vers 1 donc 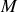tend vers 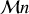: tous les dipôles s'alignent vers le champ magnétique extérieur, c'est ce qu'on appelle l'aimantation à saturation. Par contre aux températures intermédiaires, 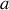tend rapidement vers zéro, comme la fonction 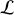et donc la susceptibilité fait de même.

Le moment dipolaire magnétique d'une molécule typique est de l'ordre du magnéton de Bohr .

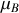Par conséquent :

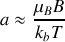
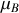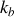Vu les ordres de grandeur de et de , pour des valeurs raisonnables de 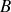en Tesla (le record est de l'ordre de 20 T) et pour 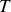proche de la température ambiante 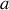est usuellement très petit. Un développement limité d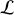e donne

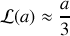
d'où :

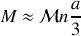
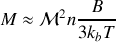
or la susceptibilité magnétique est définie par :

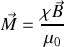
donc

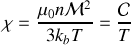
et on retrouve la loi de Curie que nous avions discutée macroscopiquement.