Dans le paragraphe précédent, nous avions supposé que toutes les projections du moment magnétique suivant la direction du champ magnétique extérieur étaient possibles.

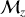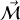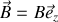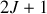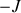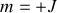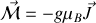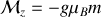Cependant, comme nous l'avons déjà discuté en partie, la théorie quantique montre que les projections de sur la direction de sont quantifiées, et ne peuvent prendre que valeurs entre et . Ainsi et avec 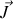moment cinétique de norme 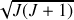et 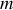un nombre entier.

Si nous supposons valable la statistique de Boltzmann et reprenons le calcul du paragraphe précédent, le nombre de dipôles magnétiques par unité de volume dans l'état 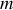, en présence d'un champ magnétique extérieur 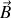vaut de nouveau, avec les mêmes notations

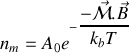
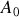( constante de normalisation et 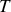température absolue du thermostat) mais cette fois en tenant compte de la quantification du moment

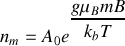
En posant

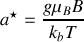
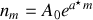
et la condition de normalisation donne, en considérant qu'il y a 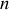dipôles par unité de volume

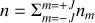
d'où

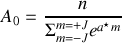
or l'aimantation est reliée à la valeur moyenne du nombre 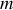qui vaut par définition

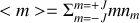
donc en substituant la valeur de

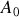
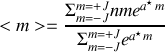
En introduisant 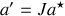par tradition, pour faire ressortir le rôle de 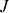on obtient

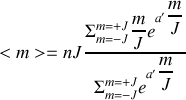
soit encore

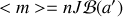
avec 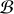la fonction dite de Brillouin.

On peut vérifier qu'aux températures usuelles on a accord avec la théorie de Langevin. Pour un système de spin à deux niveaux pour lequel 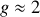par exemple

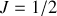( donc 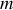peut prendre les deux valeurs 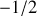et )

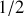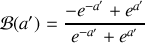
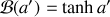
Comme 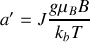on peut vérifier que même pour les valeurs extrêmes de 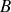(10 T par exemple) à température ambiante de 300K 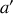est très faible donc

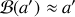
et

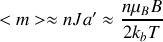
l'aimantation moyenne vaut donc par unité de volume

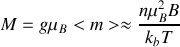
La théorie de Langevin nous avait donné

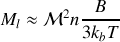
Or vectoriellement nous avions pour le moment magnétique

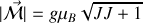
et donc ici

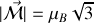
donc la théorie de Langevin conduit à

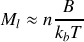
et donc au même résultat.