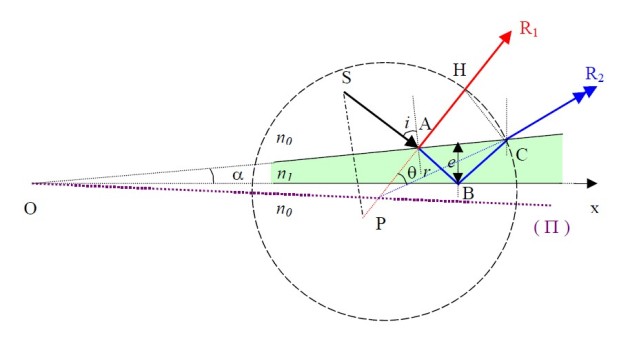
Un coin (cf. Figure 27) est réalisé à chaque fois que deux surfaces réfléchissantes ne sont pas rigoureusement parallèles entre elles mais forment un dièdre d'angle au sommet faible.

Figure 27 : Illustration du cheminement de la lumière dans un coin d'angle au sommet α

Nous observons qu'un rayon lumineux 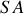se réfléchit sur le premier dioptre et est transmis 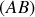dans le coin avant de se réfléchir sur le second dioptre. Les deux rayons émergents 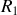et 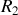ne sont pas parallèles entre eux compte tenu de l'angle du dièdre. Ils se coupent donc, non pas à l'infini, mais en un point 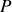qui se trouve localisé au voisinage du coin. En ce point les deux rayons se superposent avec un déphasage qui dépend principalement de l'épaisseur du coin. C'est le seul endroit ou ces rayons se superposent et c'est donc en ce point que les interférences sont observées ; pour cette raison les interférences sont dites localisées. Expérimentalement on observe une figure d'interférences constituée de franges rectilignes parallèles à l'axe du dièdre.

Cette observation est une nouvelle fois conforme à la loi de Curie sur la symétrie des effets. La présence d'un dièdre détruit la symétrie de révolution de la lame à faces parallèles et les franges adoptent la symétrie imposée par le dièdre.

Leur localisation peut être parfaitement déterminée analytiquement. Pour cela il faut trouver la position du point 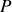de croisement des deux rayons en se rappelant que contrairement à la figure les angles 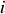et sont très petits. Dans le triangle (cf. Fig. 27) nous pouvons écrire que

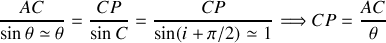
Dans le triangle 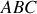nous avons

avec représentant l'angle de sortie du rayon 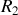par rapport à la normale au dioptre.

D'autre part dans le triangle 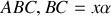( 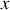étant la position du point 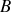par rapport à l'arête 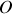du dièdre) et

d'où

Compte tenu de la faiblesse des angles, le point 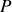est très proche de 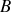et

Cela montre que l'angle 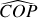ne dépend pas de 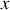et que le point 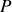est situé dans le voisinage immédiat des deux dioptres.