Nous considérons les deux rayons
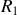 et
et
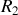 . Soit (
. Soit (
 ) le cercle de centre
) le cercle de centre
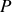 et de rayon
et de rayon
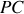 (cf. Fig. 27). Il est facile de voir qu'en
(cf. Fig. 27). Il est facile de voir qu'en
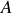 le rayon est unique et se divise en ce point. Après le passage aux points
le rayon est unique et se divise en ce point. Après le passage aux points
 et
et
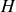 , les rayons se propagent de la même manière dans le milieu d'indice
, les rayons se propagent de la même manière dans le milieu d'indice
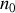 . Il s'ensuit que la différence de marche entre les deux rayons
. Il s'ensuit que la différence de marche entre les deux rayons
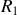 et
et
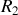 est égale à la différence de chemin optique entre les deux rayons soit :
est égale à la différence de chemin optique entre les deux rayons soit :
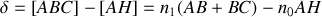
Le calcul est donc identique à celui mené pour la lame à face parallèle et conduit à
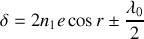
Nous considérons que le coin est éclairé en incidence quasi-normale ce qui conduit au deuxième ordre près à
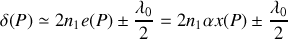
où
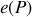 est l'épaisseur du coin à l'abscisse
est l'épaisseur du coin à l'abscisse
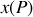 .
.
L'ordre d'interférence au point
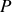 est donné par
est donné par
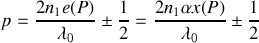
Nous voyons que, dans le cas d'un coin, l'ordre d'interférence est constant si l'épaisseur
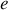 est constante. Les franges sont de ce fait qualifiées de franges d'égale épaisseur et sont aussi appelées franges de Fizeau. Comme l'épaisseur du film augmente avec l'éloignement
est constante. Les franges sont de ce fait qualifiées de franges d'égale épaisseur et sont aussi appelées franges de Fizeau. Comme l'épaisseur du film augmente avec l'éloignement
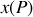 du centre du dièdre l'ordre n'est pas constant; il est minimal sur l'arête du dièdre et croît au fur et à mesure que l'on s'en éloigne.
du centre du dièdre l'ordre n'est pas constant; il est minimal sur l'arête du dièdre et croît au fur et à mesure que l'on s'en éloigne.
Remarque :
L'interfrange qui sépare deux franges consécutives de même nature est donné par
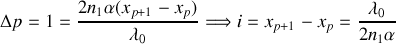
L'interfrange est donc constant et ne dépend que de l'angle du dièdre. Il croît lorsque cet angle devient très faible. Il délimite des franges rectilignes parallèles à l'axe du dièdre.




