Teinte plate et contact optique
Les figures d'interférences observables avec un interféromètre de Michelson sont celles qui correspondent à la division d'amplitude. Elles dépendent de l'orientation respectives des deux miroirs. Si ceux-ci sont à égale distance de la séparatrice et si ils sont perpendiculaires entre eux, la différence de marche entre les deux rayons est nulle. Ils se superposent en tous points du champ d'interférence avec la différence de phase
représentant la différence de phase à la réflexion. Cette différence de phase dépend très fortement de la nature des couches minces déposées sur
la séparatrice. L'observateur voit en tous points une intensité égale à
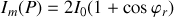
qui est donc uniforme. Cette intensité uniforme est appelée la teinte plate et elle se produit au contact optique c'est à dire à l'endroit très précis où la différence de marche est nulle. D'un point de vue expérimental la teinte plate s'obtient en “chariotant” de façon à égaliser la longueur des bras du Michelson. Cette position est définie de façon quasi-ponctuelle et le contact optique est évidemment perdu pour un déplacement infinitésimal (de l'ordre du
) du chariot.
Remarque :
La teinte observée en lumière monochromatique au contact optique ne dépend que de
.
Schéma équivalent du Michelson
Le fonctionnement d'un Michelson s'interprète facilement si l'on remplace l'un des deux miroirs par son symétrique par rapport à la séparatrice. Dans cette opération le miroir symétrique
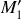du miroir
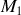est un miroir virtuel qui se trouve à la distance
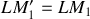de la lame.
On distingue alors deux types de fonctionnement selon l'orientation respective des
deux miroirs
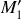et
:
la lame d'air si ces deux miroirs sont rigoureusement parallèles ce qui conduit aux franges d'égale inclinaison
le coin d'air si ces deux miroirs font un petit angle
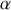entre eux ce qui conduit aux franges d'égale épaisseur
Dans le premier cas la différence de marche entre deux rayons
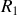et
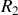qui passent par le centre de la lame est égale à
et la différence de phase entre ces deux rayons est
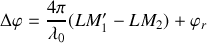
Le centre de la figure est donc alternativement brillant où sombre selon la valeur de
.
Remarque :
Si l'on considère l'ensemble des rayons issus de la source, nous constatons que le plan d'observation a la symétrie de révolution. Le problème est strictement équivalent à celui d'une lame mince d'air à faces parllèles d'indice
.
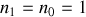L'observation des anneaux peut se faire au moyen d'une lentille mince de grande focale
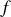ou au moyen d'une lunette réglée sur l'infini (équivalente à une lentille mince de courte focale
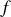). L'intensité en un point
du plan d'observation distant de
du centre est donnée par
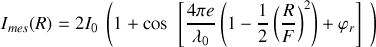
Dans le second cas le problème est celui d'un coin d'air. Les franges sont cette fois-ci rectilignes et parallèles à l'arête du coin d'air. La différence de marche en un point
de l'écran situé à la position
du centre est égale à
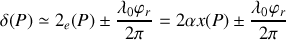
et l'intensité au point
est égale à
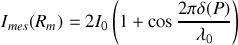
L'observation se fait soit à la lunette soit en projetant les franges localisées du coin d'air avec une lentille mince de focale
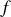. Les franges dans ce cas sont agrandies d'un facteur
avec
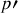la distance de la lentille à l'écran et
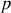la distance de la lentille au coin d'air.
Franges rectilignes du coin d'air obtenues en inclinant le miroir
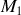d'un angle
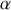par rapport au miroir
dans un interféromètre de Michelson. L'éclairage est réalisé avec une lampe à vapeur de sodium
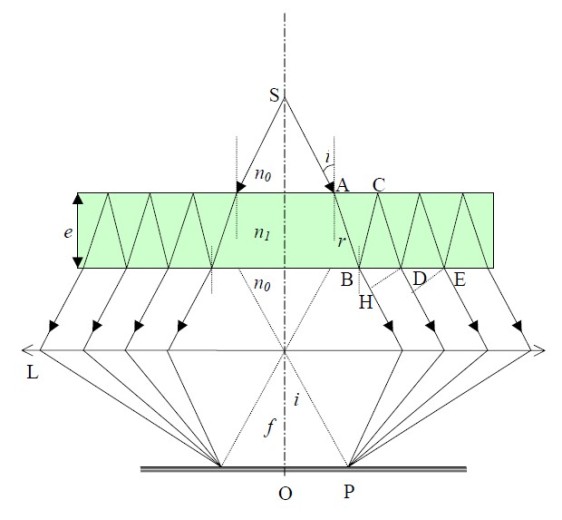
Transmission de
ondes à travers une lame mince d'épaisseur
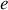et d'indice
