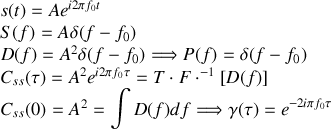Le signal lumineux idéalement cohérent est par définition l'onde plane sinusoïdale monochromatique. Une telle onde se propage avec un vecteur d'onde unique de propagation et n'est pas limitée dans le temps. Elle est décrite par la relation
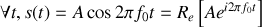
La transformée de Fourier de ce signal conduit à une distribution de Dirac et s'écrit
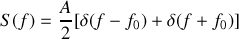
Il est clair que le signal sinusoïdal idéalement cohérent n'est pas un signal à énergie finie. En effet comme il est de durée illimitée l'intégrale
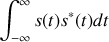
ne converge pas.
La fonction de corrélation de ce signal s'obtient donc en intégrant sur une période le produit des signaux décalés ce qui conduit à
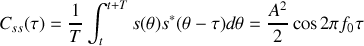
Propriété :
Nous constatons donc que la fonction d'autocorrélation de ce signal est une fonction sinusoïdale de
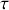. Il s'ensuit que si le signal est idéalement cohérent il est possible de le corréler dans le temps périodiquement avec lui-même.
Nous verrons que cette propriété est l'essence même du phénomène d'interférence lumineuse. En effet dans une expérience d'interférence, on superpose un signal lumineux à un autre signal décalé dans le temps.
Remarque :
Si les signaux qui se superposent sont des signaux idéalement cohérents nous voyons que quel que soit
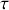il sera possible de corréler ces signaux et que la fonction de corrélation passera par des maxima et minima d'intensité selon la valeur de
.
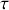Complément :
Si nous considérons maintenant la fonction de corrélation au temps
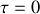, nous avons
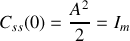
Nous voyons d'autre part que le théorème de Wiener est bien vérifié puisque la transformée de Fourier de la fonction d'autocorrélation du signal est bien égale au module au carré de la transformée de Fourier du signal. En effet nous avons
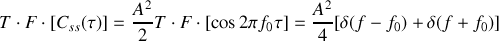
Remarque :
Si le signal sinusoïdal est décrit par une exponentielle complexe alors
