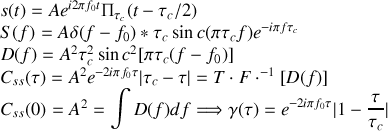Il s'agit d'un signal sinusoïdal d'extension finie dans le temps. Compte tenu de l'existence de ce signal pendant un temps fini, on parle de train d'onde dont les caractéristiques importantes sont sa durée
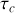et la période
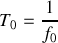du signal sinusoïdal à partir duquel il est construit. L'expression mathématique du train d'onde est obtenue en faisant le produit d'un signal idéalement cohérent par un porte de largeur finie
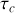ce qui aboutit à
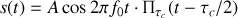
L'allure du train d'onde est représentée sur la figure
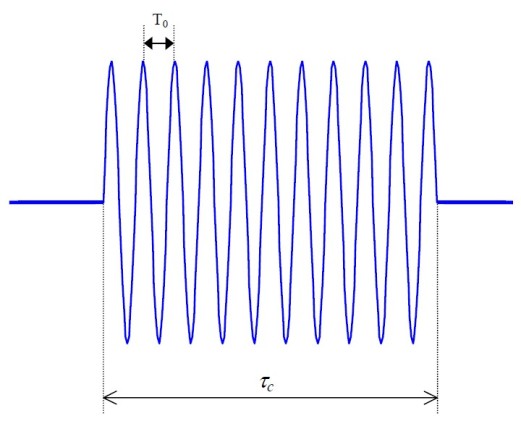
L'utilisation d'un train d'onde est justifiée par le fait que les atomes n'émettent de la lumière de façon cohérente que pendant un temps fini.
Rappel :
Le mécanisme d'émission radiative repose sur l'excitation de niveaux électroniques d'un atome. L'atome se désexcite en émettant pendant un temps fini un train d'onde lumineux présentant une fréquence propre
.
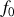La largeur de la porte définit ce qu'on appelle le temps de cohérence
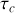du signal ce que nous allons justifier au moyen des calculs qui vont suivre.
La transformée de Fourier de ce signal nous indique immédiatement que la troncature temporelle du signal idéalement cohérent a d'importantes répercussions sur le spectre du signal. Il est facile de vérifier en utilisant le théorème de Plancherel (sur la transformée de Fourier d'un produit) que
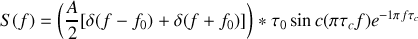
En remarquant que la distribution de Dirac est le neutre de la convolution, il vient
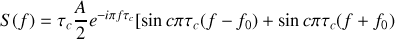
La conséquence immédiate d'un tel résultat est que le spectre d'un train d'onde sinusoïdal n'est pas décrit par une fréquence unique mais par la fonction sinus cardinal qui décroît rapidement quand on s'éloigne de la fréquence propre du signal. Le premier zéro de cette fonction est localisé en
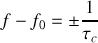
ce qui montre que l'étendue spectrale de
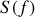est inversement proportionnelle à la durée
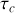du train d'onde. Il s'ensuit que si le train d'onde est de durée infinie le spectre devient un pic de Dirac et l'on retrouve alors le résultat précédent. Dans le cas contraire, le spectre est d'autant plus étendu que le temps de cohérence du train d'onde est court. Un train d'onde sinusoïdal centré sur la fréquence
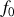n'est donc pas monochromatique.
La densité spectrale du train d'onde s'écrit
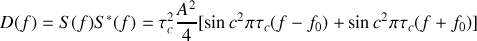
car on admet que le produit croisé est quasi nul pour autant que
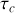ne soit pas trop petit.
Nous pouvons également accéder à la fonction d'autocorrélation du signal qui s'écrit compte tenu du fait que le signal est à énergie finie
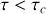
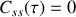si
si
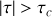
Nous voyons sur la figure que la fonction de corrélation est non nulle si le signal
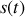se recouvre avec le signal
.
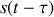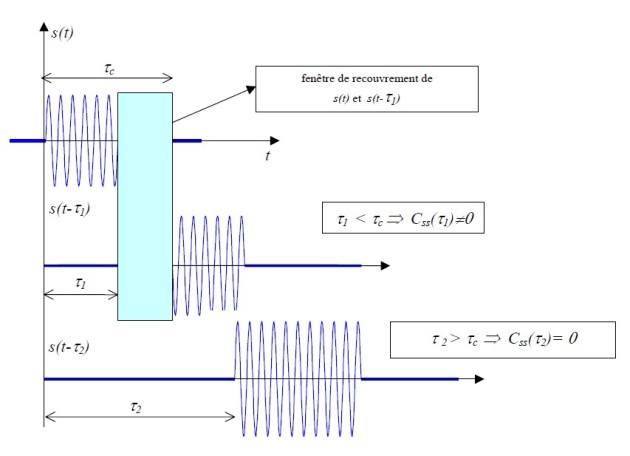
Ce résultat montre de façon éclatante que la fonction de corrélation ne peut prendre une valeur non nulle que si le décalage temporel que l'on fait subir aux signaux qui se superposent est inférieur à la durée du train d'onde. Pour cette raison la durée du train d'onde représente également le temps de cohérence du signal lumineux. On lui associe une longueur de cohérence qualifiée de longueur de cohérence temporelle dont la valeur est donnée par la distance parcourue par l'onde pendant la durée de ce train d'onde soit
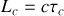
L'utilisation de la relation 7.32 montre que la longueur de cohérence est aussi donnée par
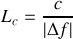
et comme
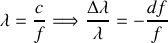
il s'ensuit que
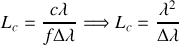
Nous voyons donc au travers de cette expression que la longueur de cohérence temporelle est donc directement liée à la dispersion en longueur d'onde du spectre de la source lumineuse.
Attention :
En particulier nous retiendrons qu'une onde rigoureusement monochromatique correspond à un train d'onde de durée infinie. Toute réduction de la durée de vie du train d'onde se traduit par un élargissement du spectre
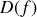et par une longueur de cohérence temporelle finie.
Nous constatons que la fonction de corrélation de trains d'onde de durée finie comporte une fonction oscillante dont l'enveloppe décroît linéairement en fonction de
.
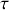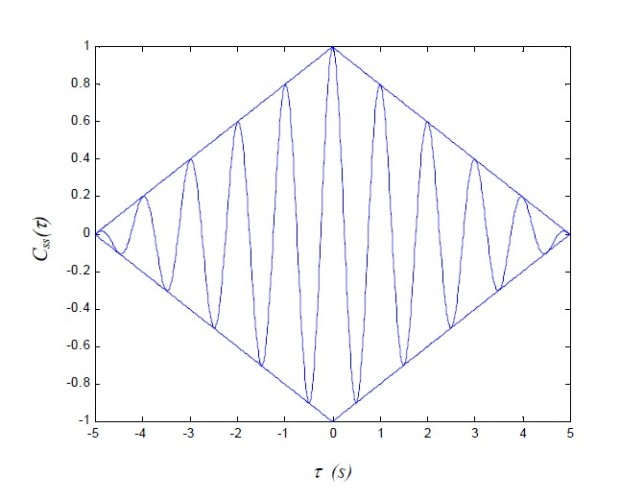
Cette décroissance linéaire résulte de l'utilisation d'une fonction porte pour limiter l'expansion temporelle du signal. En particulier cela signifie que si l'on est capable d'accéder à la représentation graphique de
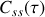et que l'on observe dans cette représentation une décroissance linéaire d'une fonction oscillante on pourra alors affirmer que le signal émis par la source est un train d'onde sinusoïdal. Nous verrons par la suite que la mesure de la fonction d'autocorrélation ne conduit pas nécessairement à une fonction oscillante dont l'enveloppe décroît linéairement. Le train d'onde sinusoïdal n'est donc pas la seule façon de se représenter un signal lumineux quasi-monochromatique.
De façon analogue à ce que nous avions fait pour le signal idéalement cohérent on peut décrire le train d'onde par une exponentielle complexe ce qui conduit à
