La densité spectrale 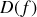représente la répartition de l'intensité de la source en fonction de la fréquence. C'est une quantité directement accessible à l'expérience puisque sa mesure est obtenue en utilisant un spectroscope à prisme ou à réseau. Pour cela il suffit de disposer d'une fente lumineuse source au foyer d'une lentille convergente. L'onde plane issue de la lentille est dispersée par le réseau et est refocalisée au foyer d'une lentille convergente. Le spectre est observé sur un écran ou à travers une lunette de visée. Le spectre que l'on obtient par cette technique n'est pas le spectre vrai de la source mais représente la convolution du spectre vrai par la fonction de résolution du spectroscope. Le spectre d'une source lumineuse est une signature de la source etsa connaissance permet de remonter par le calcul à la transformée de Fourier inverse à la fonction d'autocorrélation 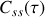du signal lumineux. Nous verrons cependant que la fonction 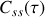est accessible de façon beaucoup plus fine par une autre méthode. Nous présentons quelques exemples de spectres en précisant leur domaine de validité.

• onde plane monochromatique idéalement cohérente

La densité spectrale est composée d'un pic de Dirac localisé à la fréquence de la radiation utilisée

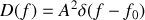
Ce type de spectre est idéal et ne peut jamais être mesuré. C'est la représentation limite du spectre issu d'un laser monomode.

• doublet idéalement cohérent

C'est la superposition de deux ondes monochromatiques idéalement cohérentes. Le spectre est composé de deux distributions de Dirac centrées sur les fréquences d'émission des deux ondes. Ces deux fréquences sont supposées en général très proches l'une de l'autre

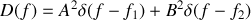
Ce type de spectre est idéal et ne peut jamais être mesuré. C'est la représentation limite du spectre d'une lampe à vapeur de sodium qui contient un doublet à 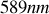et .

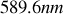• train d'onde sinusoïdal idéal

Le spectre est étendu à cause de la durée finie du train d'onde. Nous avons vu qu'il est défini par

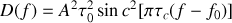
Ce spectre se rapproche plus de la réalité pour décrire des sources monochromatiques. Toutefois le train d'onde est souvent amorti et la forme du spectre dévie en général de la fonction sinus carré cardinal. Ce type de spectre est utile pour modéliser simplement des signaux lumineux d'extension temporelle finie.