Ce coefficient peut être directement mesuré en utilisant une expérience d'interférences et plus particulièrement l'interféromètre de Michelson. Elle consiste à utiliser l'interféromètre de Michelson monté en lame mince parallèle en mesurant l'intensité au centre en fonction de l'épaisseur
de la lame mince.
Rappel :
Dans ce type d'appareil lorsque les deux miroirs sont perpendiculaires entre eux l'intensité que l'on mesure au foyer de la lentille de projection est donnée par
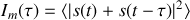
En effet le signal incident se divise en amplitudes égales en passant par la séparatrice. Les deux ondes ainsi séparées ont exactement les mêmes caractéristiques à la sortie de la séparatrice qui a pour effet de cloner l'onde incidente. Les deux clones cheminent vers les deux miroirs
et
et se recombinent après un aller-retour sur leurs trajets respectifs. Si les deux miroirs sont à égale distance de la séparatrice les deux ondes clonées parcourent la même distance avant de se recombiner. Par contre si les deux miroirs ne sont pas à égale distance mais présentent un écart
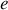, l'une des deux ondes va parcourir une distance égale au double de cet écart et arrivera au point de recombinaison avec un décalage temporel
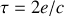par rapport à l'autre onde. L'interféromètre de Michelson agit comme un diviseur, déphaseur et sommateur d'onde lumineuse. Le récepteur lumineux joue le rôle de corrélateur car il est sensible à
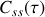. Un interféromètre de Michelson est donc un corrélateur d'ondes lumineuses et il permet d'accéder à la fonction
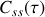. Nous avons en effet vu que
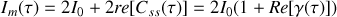
Pour une onde plane monochromatique incidente idéale
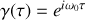. L'intensité mesurée est donc
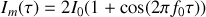
et la fonction de contraste est donc maximale puisque
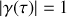. Dans ce cas très simple l'intensité oscille alternativement entre un maximum d'intensité
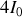et un minimum nul selon la valeur de l'écart entre les deux miroirs.
Pour le train d'onde sinusoïdal, nous avons
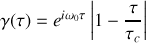si
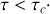. Il s'ensuit que l'intensité mesurée s'écrit
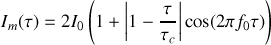
Attention :
Le facteur de contraste
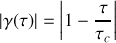ce qui montre qu'il diminue avec
.
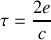Remarque :
Les franges sont sont initialement bien contrastées puis de moins en moins visibles au fur et à mesure que l'on déplace le chariot. Quand la valeur de
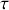atteint la valeur
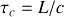la visibilité des franges s'annule et l'intensité devient alors uniforme pour toute augmentation ultérieure de
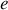: les deux trains d'onde ne peuvent plus interférer.
Si l'on suppose maintenant que le Michelson n'est pas éclairé par une onde monochromatique mais par une distribution d'ondes de différentes fréquences on peut voir que dans l'expression générale
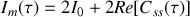
les deux parties de la somme s'indentifient à
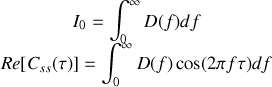
L'intensité mesurée est donc
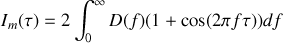
Le coefficient de cohérence peut donc être obtenu en effectuant l'opération suivante
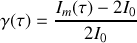
Remarque :
L'interféromètre de Michelson est l'instrument le plus approprié à cette mesure du coefficient de cohérence.
En effet on peut imaginer que dans toute expérience d'interférence il est possible d'accéder à cette quantité puisque l'on superpose des signaux décalés dans le temps. Ce serait méconnaître les limitations expérimentales des dispositifs utilisant la division du front d'onde que de croire qu'il peuvent permettre la mesure de
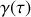. En effet ces dispositifs sont d'une part très sensibles à la cohérence spatiale de la source (voir chapitre suivant) et à la diffraction par de petites ouvertures qui masquent le contraste des franges d'interférence. D'autre part le décalage temporel que l'on peut raisonnablement mesurer dans ce type d'expérience reste toujours très faible.
Exemple :
On peut considérer l'expérience des trous d'Young. Dans une expérience de ce type les franges d'interférences sont rarement mesurables au delà de l'ordre 100 à cause du phénomène de diffraction. Le champ est donc de l'ordre de
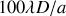et les ondes qui interfèrent à l'ordre 100 subissent une différence de chemin optique de
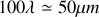. Pour de nombreuses sources lumineuses, la longueur de cohérence temporelle est nettement supérieure (de l'ordre de
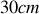pour un laser
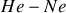) et la cohérence temporelle n'est donc pas réellement mesurable car son effet n'est pas visible.
Dans une expérience de division d'amplitude utilisant l'interféromètre de Michelson, la cohérence spatiale de la source ne joue pas vraiment et le déplacement du chariot porteur de l'un des miroirs peut se faire sur une large course. Avec cet instrument on peut donc mesurer l'intensité sur une grande plage de valeurs de
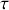ce qui permet d'accéder à la cohérence temporelle de la source.
