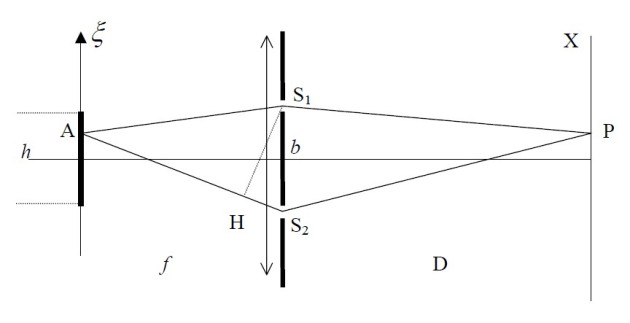
Source ponctuelle
Nous reprenons les fentes d'Young en supposant que la source qui éclaire les fentes est ponctuelle et parfaitement monochromatique (cohérence temporelle parfaite) de fréquence
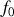 . Elle est située sur l'axe optique du système ce qui fait que la différence de marche qui existe au point
. Elle est située sur l'axe optique du système ce qui fait que la différence de marche qui existe au point
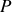 d'observation provient uniquement de la différence de trajet optique
d'observation provient uniquement de la différence de trajet optique
 . Nous supposons en outre que les fentes sont très fines ce qui permet de s'affranchir de la contribution de la diffraction. Nous appelons
. Nous supposons en outre que les fentes sont très fines ce qui permet de s'affranchir de la contribution de la diffraction. Nous appelons
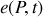 le champ scalaire au point
le champ scalaire au point
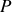 Nous avons donc
Nous avons donc
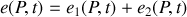
Les champs scalaires
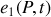 et
et
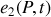 se déduisent des champs émis à la source en tenant compte du retard accumulé au cours de la propagation. Nous pouvons donc écrire que
se déduisent des champs émis à la source en tenant compte du retard accumulé au cours de la propagation. Nous pouvons donc écrire que
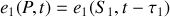 avec
avec
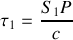
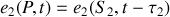 avec
avec
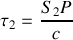
Si l'on prend arbitrairement l'origine des phases dans le plan des sources secondaires
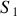 et
et
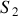 qui sont en phase à l'issue de la duplication de l'onde issue de
qui sont en phase à l'issue de la duplication de l'onde issue de
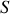 , nous voyons que
, nous voyons que
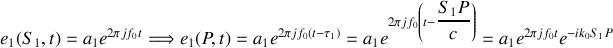
Il en va de même pour le champ
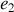 si l'on remplace l'indice 1 par 2.
si l'on remplace l'indice 1 par 2.
Si l'on s'intéresse à l'intensité mesurée au point
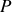 nous voyons que
nous voyons que
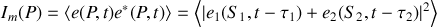
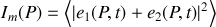
Le calcul direct a déjà été fait au premier chapitre et il est facile de montrer que
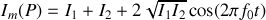 avec
avec
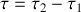
Nous pouvons aussi procéder de façon plus formelle en utilisant les fonctions de corrélation définies au chapitre précédent. En effet observer des interférences en un point
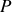 quelconque d'un écran n'est rien d'autre que de superposer deux signaux décalés dans le temps. Comme seule l'intensité est mesurable la figure d'interférences contient directement l'information sur la fonction de corrélation entre les deux signaux qui se superposent.
quelconque d'un écran n'est rien d'autre que de superposer deux signaux décalés dans le temps. Comme seule l'intensité est mesurable la figure d'interférences contient directement l'information sur la fonction de corrélation entre les deux signaux qui se superposent.
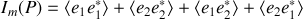
Nous avons vu dans le chapitre précédent que
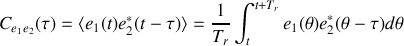
et nous avons à calculer
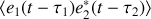 . En posant
. En posant
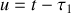 , il est facile de voir que
, il est facile de voir que
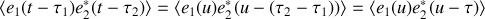
Il s'ensuit que
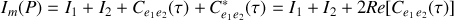
En faisant apparaître le degré de corrélation
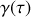 il vient
il vient
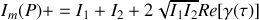
Pour des fentes de même ouverture il est clair que
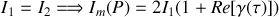
Si de plus la source est monochromatique, le calcul conduit à
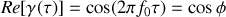
ce qui montre que les signaux issus des deux sources secondaires
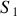 et
et
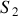 sont périodiquement corrélés.
sont périodiquement corrélés.
Remarque :
Le degré de cohérence n'est rien d'autre que le cosinus du déphasage entre les deux ondes qui se superposent en
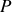 .
.
En effet quand le point
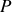 se déplace sur l'axe des
se déplace sur l'axe des
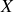 en s'éloignant de l'origine, cela revient à sommer en ce point des signaux qui sont de plus en plus décalés dans le temps. Le contraste est alors maximum puisque
en s'éloignant de l'origine, cela revient à sommer en ce point des signaux qui sont de plus en plus décalés dans le temps. Le contraste est alors maximum puisque
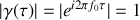 . Cela veut simplement dire que les ondes issues de
. Cela veut simplement dire que les ondes issues de
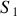 et
et
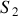 peuvent interférer quelle que soit la différence de marche. C'est une conséquence de l'utilisation d'une source de cohérence temporelle idéale. Une telle source même ponctuelle n'existe pas et donc a fortiori elle n'existera pas non plus si elle est étendue.
peuvent interférer quelle que soit la différence de marche. C'est une conséquence de l'utilisation d'une source de cohérence temporelle idéale. Une telle source même ponctuelle n'existe pas et donc a fortiori elle n'existera pas non plus si elle est étendue.
Le calcul que nous venons de reprendre avait pour but de bien montrer que dans l'expérience classique des fentes d'Young, le résultat que l'on observe à l'écran dépend du degré de cohérence de la source. Jusqu'à présent seule la cohérence temporelle est prise en compte. La cohérence spatiale s'aborde en considérant une source étendue.
Rappel :
Si la source se trouve au foyer d'une lentille de distance focale
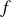 en un point
en un point
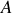 de position
de position
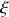 en dehors de l'axe optique il faut tenir compte d'un déphasage supplémentaire
en dehors de l'axe optique il faut tenir compte d'un déphasage supplémentaire
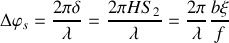
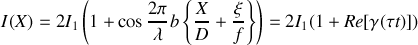
Nous allons montrer quelle est l'influence d'une source étendue sur la visibilité des franges d'interférences.
Source étendue
On peut maintenant se poser la question de savoir quelle sera l'allure de la figure d'interférences si la source est étendue. On suppose que la source possède une spectre centré sur la fréquence
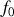 mais que sa cohérence temporelle est finie et inférieure au temps d'intégration du détecteur. Dans ce cas deux points voisins de la source que nous appellerons
mais que sa cohérence temporelle est finie et inférieure au temps d'intégration du détecteur. Dans ce cas deux points voisins de la source que nous appellerons
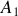 et
et
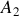 ne présentent pas de relation de phase entre eux et l'intensité provenant du point source
ne présentent pas de relation de phase entre eux et l'intensité provenant du point source
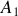 viendra donc s'ajouter à l'intensité venant du point source
viendra donc s'ajouter à l'intensité venant du point source
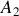 . Si l'on ne considère que ces deux points on a alors au point
. Si l'on ne considère que ces deux points on a alors au point
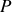 d'interférence
d'interférence
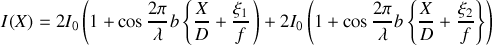
Si maintenant on considère la source comme continûment étendue sur une distance
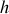 nous voyons que l'intensité au point
nous voyons que l'intensité au point
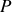 sera donnée par
sera donnée par
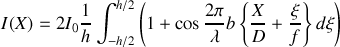
Nous supposons en particulier que sur la hauteur totale
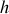 de la source lumineuse l'intensité est
de la source lumineuse l'intensité est
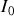 . Pour une tranche
. Pour une tranche
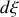 de la source l'intensité est donc proportionelle à
de la source l'intensité est donc proportionelle à
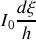 . Il s'ensuit que
. Il s'ensuit que
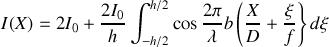
Evaluons cette intégrale en passant à la notation complexe
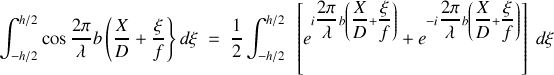
soit
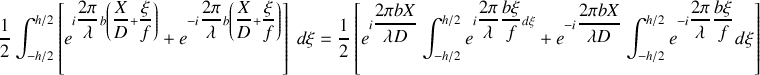
Ceci conduit finalement à
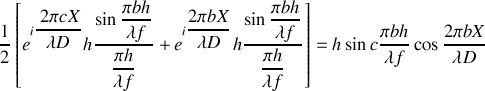
Il s’ensuit que l’intensité au point
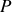 s’écrit alors
s’écrit alors
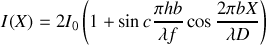
La figure d'interférence est donc altérée par l'extension de la source. Si l'on compare cette expression avec le résultat obtenu au chapitre précédent où nous avons démontré que
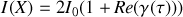
on voit que
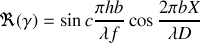
Le facteur de contraste est donné par
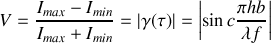 (9)
(9)
Remarque :
La présence de la fonction sinus cardinal dans l'expression de la visibilité des franges laisse penser que ce facteur est lié à la transformée de Fourier de la fente source.
Nous verrons que cela est en effet prédit par le théorème de Zernicke et Van Cittert.
En particulier, les franges deviennent complètement brouillées si
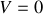 . L'équation 9 montre que cette condition est vérifiée si
. L'équation 9 montre que cette condition est vérifiée si
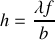
Remarque :
Le brouillage des franges se produit quand la distance
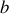 de séparation des fentes d'Young est égale à la valeur du premier lobe de diffraction généré par la source de dimension
de séparation des fentes d'Young est égale à la valeur du premier lobe de diffraction généré par la source de dimension
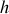 . Les franges seront bien visibles si le lobe de diffraction est beaucoup plus large que la distance de séparation des fentes.
. Les franges seront bien visibles si le lobe de diffraction est beaucoup plus large que la distance de séparation des fentes.
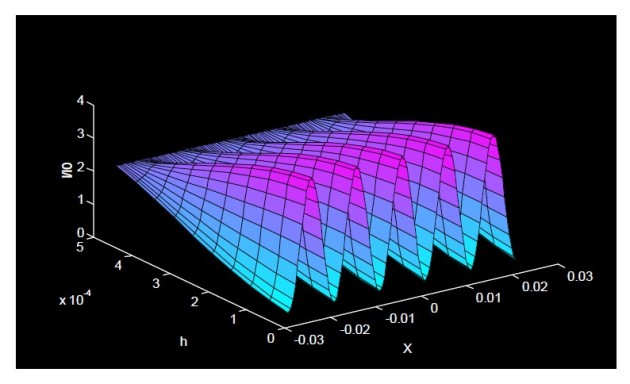
La figure 56 représente l'évolution du contraste (de la visibilité) des franges d'interférences en fonction de la hauteur
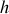 de la source avec
de la source avec
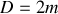 ,
,
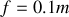 ,
,
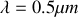 et
et
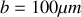 . On constate sur cette figure qu'au delà d'une certaine valeur, les franges se brouillent.
. On constate sur cette figure qu'au delà d'une certaine valeur, les franges se brouillent.
Cette étude montre que la visibilité des franges d'interférences dépend de l'étendue spatiale de la source. Quand la source présente un diamètre angulaire très faible
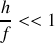 , les ondes issues de la source sont spatialement cohérentes.
, les ondes issues de la source sont spatialement cohérentes.
Remarque :
Il n'y aura pas brouillage des franges si l'argument de la fonction sinus cardinal est faible devant
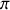 soit
soit
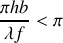
Complément :
Si l'on introduit l'angle
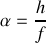 encore appelé le rayon angulaire sous lequel on voit la fente source du centre des fentes d'Young (ou du centre optique de la lentille), la condition de bonne visibilité s'écrit
encore appelé le rayon angulaire sous lequel on voit la fente source du centre des fentes d'Young (ou du centre optique de la lentille), la condition de bonne visibilité s'écrit
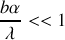
Cette inégalité fait intervenir une longueur caractéristique
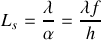
appelée longueur de cohérence spatiale de la source vue du système interférentiel. Cette quantité n'est évidemment pas intrinsèque à la source mais dépend essentiellement de la façon dont la source est collimatée. Pour observer une bonne visibilité des franges il faut une source lumineuse quasi ponctuelle puisqu'il faut imposer
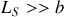
Pour augmenter la longueur de cohérence spatiale dans un dispositif interférentiel il faut clairement diminuer le rayon angulaire
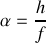 de la source ce qui peut se faire en :
de la source ce qui peut se faire en :
diminuant la taille
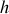 de la source
de la source
éloignant la source du dispositif interférentiel.
Dans notre exemple la visibilité sera bonne si
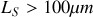 , ce qui impose comme l'indique la figure 56 une source d'extension
, ce qui impose comme l'indique la figure 56 une source d'extension
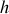 vérifiant
vérifiant
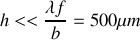
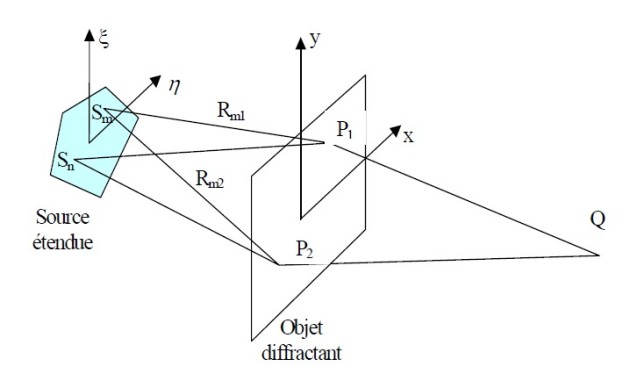
Représentation du cheminement des rayons lumineux issus de 2 points
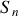 et
et
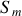 d'une même source jusqu'à leur superposition au point d'observation
d'une même source jusqu'à leur superposition au point d'observation
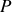
Remarque :
La longueur de cohérence spatiale des ondes issues de la source est donnée par la demi-largeur du lobe principal de diffraction de la source.