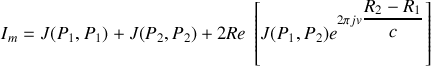Ce théorème est une généralisation de ce que nous venons de montrer sur un cas particulier. Nous considérons une source étendue
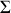 contenue dans le plan
contenue dans le plan
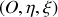 . Chaque point de cette source émet une radiation monochromatique (spectre centré sur
. Chaque point de cette source émet une radiation monochromatique (spectre centré sur
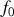 ) avec une cohérence temporelle finie. Différents points de la source sont donc incohérents entre eux. En d'autres termes il n'existe pas de relation de phase stable dans le temps entre le champ émis par un point de la source et son voisin. Nous cherchons à déterminer le champ en un point
) avec une cohérence temporelle finie. Différents points de la source sont donc incohérents entre eux. En d'autres termes il n'existe pas de relation de phase stable dans le temps entre le champ émis par un point de la source et son voisin. Nous cherchons à déterminer le champ en un point
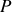 de l'objet diffractant ainsi que le degré de corrélation qui existe entre deux points de cet objet. Le but est de prédire ce qui se passera en un point unique
de l'objet diffractant ainsi que le degré de corrélation qui existe entre deux points de cet objet. Le but est de prédire ce qui se passera en un point unique
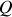 du détecteur. Nous décomposons donc la source
du détecteur. Nous décomposons donc la source
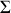 en sources élémentaires
en sources élémentaires
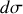 qui émettent des ondes sphériques.
qui émettent des ondes sphériques.
Par la suite nous noterons
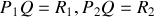
En
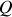 le champ scalaire est le résultat de la surperposition des champs issus des point
le champ scalaire est le résultat de la surperposition des champs issus des point
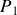 et
et
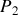 soit
soit
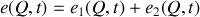
avec
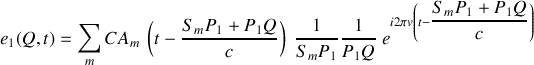
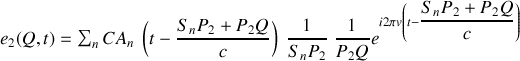
Il est clair que dans l'expression du champ en
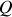 on peut sortir du signe somme les termes indépendant de l'indice de sommation soit
on peut sortir du signe somme les termes indépendant de l'indice de sommation soit
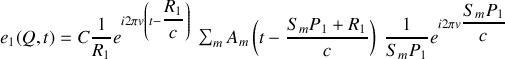
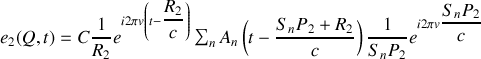
L'intensité que l'on mesure au point
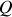 est donnée par
est donnée par
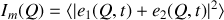
soit
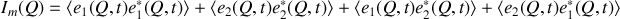
Commençons par analyser le premier terme de cette somme.
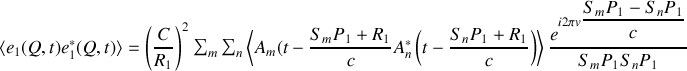
Dans cette expression
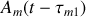 est l'amplitude complexe du champ au point
est l'amplitude complexe du champ au point
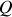 ; cette amplitude tient compte d'un terme de phase à la source qui décrit l'émission de l'onde par le point source
; cette amplitude tient compte d'un terme de phase à la source qui décrit l'émission de l'onde par le point source
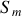 . Les ondes émises par les différents points de la source sont incohérentes entre elles ce qui signifie que la différence de phase entre l'onde émise par la point
. Les ondes émises par les différents points de la source sont incohérentes entre elles ce qui signifie que la différence de phase entre l'onde émise par la point
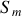 et celle émise par le point
et celle émise par le point
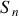 est aléatoire dans le temps. Il est donc clair que
est aléatoire dans le temps. Il est donc clair que
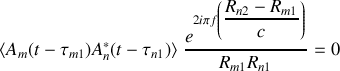 si
si
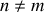
et
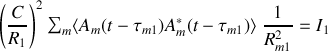 si
si
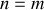
Il en va de même pour le deuxième terme qui prend la valeur
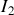 .
.
Le calcul est un peu plus compliqué pour les termes croisés qui font intervenir les points
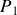 et
et
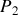 . Le raisonnement sur l'incohérence des points sources tient toujours et nous avons donc
. Le raisonnement sur l'incohérence des points sources tient toujours et nous avons donc
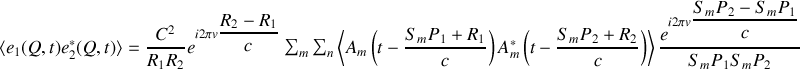
Remarque :
La double somme qui intervient dans ce calcul est appelée fonction de cohérence mutuelle des deux points
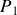 et
et
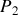 , et est notée
, et est notée
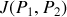
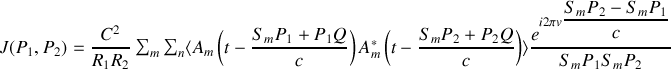
Nous avons donc
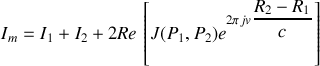
Dans ce calcul
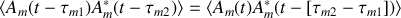
Nous faisons l'hypothèse que
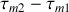 est une quantité petite devant le temps de cohérence de la source. Il s'ensuit que
est une quantité petite devant le temps de cohérence de la source. Il s'ensuit que
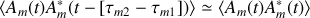
Ce qui conduit à
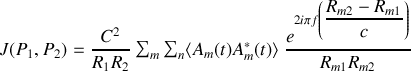
Nous considérons à juste titre que la somme discrète sur l'ensemble des points de la source peut être remplacée par une intégrale sur sa surface. Pour cela nous posons
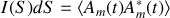
Il s'ensuit que
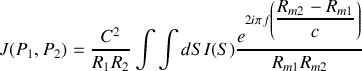
Nous pouvons évidemment considérer la fonction de cohérence mutuelle d'un point avec lui même donnée par
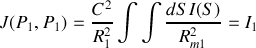
et faire apparaître ainsi apparaître le degré de corrélation mutuelle entre les points
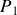 et
et
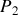
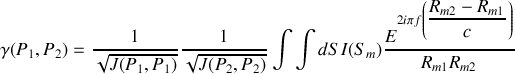
Nous constatons que le coefficient de corrélation mutuelle est très semblable à l'expression du champ diffracté par une ouverture donné par le principe de Huygens-Fresnel à ceci près que l'intégrale porte sur la surface de la source et que les distances mises en jeu partent d'un point de la source vers deux points
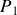 et
et
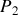 de l'objet diffractant. Dans tous les problèmes que nous traiterons l'intensité délivrée par la source sera uniforme ce qui impose
de l'objet diffractant. Dans tous les problèmes que nous traiterons l'intensité délivrée par la source sera uniforme ce qui impose
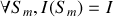
Si l'on appelle
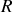 la distance qui sépare le centre de la source à celui de l'objet diffractant,
la distance qui sépare le centre de la source à celui de l'objet diffractant,
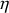 ,
,
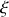 les coordonnées d'un point de la source et
les coordonnées d'un point de la source et
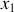 ,
,
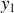 ,
,
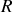 les coordonnées de
les coordonnées de
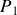 , il est facile de vérifier que
, il est facile de vérifier que
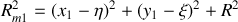
La distance
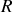 est supposée très grande par rapport aux dimensions des ouvertures ce qui impose
est supposée très grande par rapport aux dimensions des ouvertures ce qui impose
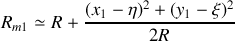
Nous pouvons donc donner une expression approchée de l'intégrale car
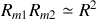
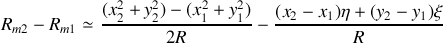
Ces approximations conduisent à
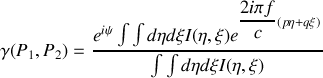
avec
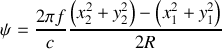
et
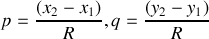
Nous voyons ainsi que le degré de cohérence mutuelle est égal à la transformée de Fourier normalisée de la distribution d'intensité de la source. Ceci constitue le théorème de Zernike-Van Cittert.
Il est clair que si les points qui diffractent sont à égale distance de l'axe optique du système
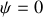 . Dans ce cas nous avons
. Dans ce cas nous avons
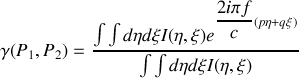
Le degré de cohérence mutuelle entre les ondes issues de la source étendue passant par les points
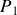 et
et
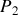 est alors égal à la transformée de Fourier normalisée de la distribution d'intensité dans la source. La transformation de Fourier est effectuée en fonction des fréquences spatiales
est alors égal à la transformée de Fourier normalisée de la distribution d'intensité dans la source. La transformation de Fourier est effectuée en fonction des fréquences spatiales
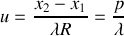
et
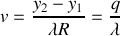
Nous concluons ainsi que l'intensité mesurée au point
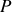 peut s'écrire
peut s'écrire