Dans le chapitre précédent, nous avons étudié l'effet de la distribution spectrale sur la figure d'interférences. Nous avons établi qu'une source présentait une cohérence temporelle d'autant meillleure que sa distribution spectrale se rapprochait de la distribution de Dirac. En particulier nous avons montré que la cohérence temporelle de la source peut être décrite par la longueur de cohérence temporelle définie par 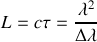. Cette longueur est la distance qu'il faut parcourir dans le sens de propagation de l'onde pour décorréler deux trains d'onde issues de la même source ; on parle aussi de cohérence longitudinale de l'onde. Dans l'approche précédente nous avions supposé que le faisceau lumineux était parfaitement collimaté c'est à dire qu'il pouvait être assimilé à une onde quasi-plane. Dans ce cas la phase de l'onde est la même en tous points d'un plan perpendiculaire à la direction de propagation et l'on admet alors que la cohérence du faisceau est parfaite dans ce plan. La cohérence dans le plan perpendiculaire à la direction de propagation est appelée cohérence spatiale du faisceau. Si le faisceau n'est pas collimaté ou si l'on utilise une source étendue, l'onde lumineuse présente une phase qui varie dans un plan perpendiculaire à la direction de propagation. Tant que cette variation de phase reste faible par rapport à 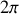on admet que les ondes restent corrélées. La distance qu'il faut parcourir pour perdre cette corrélation est appelée longueur de cohérence spatiale ou longueur de cohérence transversale. Nous allons examiner dans ce chapitre comment définir cette longueur et comment la mesurer. Nous établirons ensuite quelles sont les conditions optimales d'observation d'une figure d'interférences.