Mathématiquement si l'on considère un point
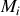d'une surface d'onde appartenant à une source secondaire, la contribution de Fresnel aboutit à ce que le champ
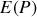au point d'observation
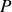soit donné par :
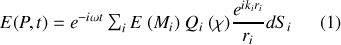
Le terme en
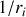signifie que l'on considère la propagation d'ondelettes sphériques, le terme exponentiel est un terme de déphasage entre le point source
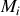de la surface diffractante et le point
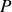, le terme
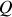appelé facteur d'obliquité ou d'inclinaison est lié à l'angle
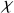entre la direction de propagation de l'onde incidente et la direction de l'onde diffractée et
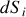est la surface élémentaire qui diffracte au point source
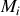. Le facteur d'obliquité est maximal en
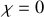et décroit rapidement avec
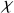pour s'annuler en
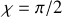. Il est possible de démontrer que ce facteur est lié à une constante multiplicative près au cosinus de l'angle
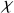.Le champ total au point
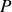résulte de la superposition de tous les champs provenant des sources élémentaires.
Fondamental :
La répartition lumineuse étant continue dans la surface
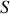, la somme discrète de l'équation (1) est remplacée par une intégrale double sur l'étendue de la surface qui diffracte et cette expression se transforme en :
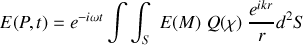
L'intégrale que nous venons d'obtenir s'appelle l'intégrale de Fresnel-Kirchhoff. Elle constitue l'essence mathématique de tous les phénomènes de diffraction et plus généralement de diffraction et interférence.
Si l'on considère que l'angle
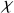est toujours très petit ce qui constitue l'approximation des rayons paraxiaux (faiblement inclinés sur l'axe optique du système) alors
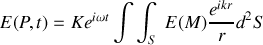
Il peut être judicieux de remarquer que le terme de phase
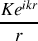fait intervenir le passage du point
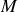au point
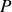d'observation et peut être écrit sous la forme d'une fonction de transfert
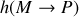de
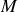en
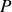
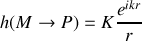
Il s'ensuit que l'intégrale de Fresnel Kirchhoff devient
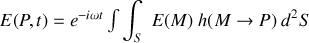
Si l'on se base sur une source
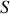lumineuse ponctuelle (partie droite de la figure 5) le champ en
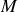est donné par
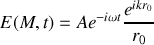
ce qui conduit à
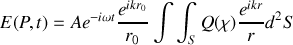
Attention :
L'intégrale ci-dessus n'est pas simple à calculer et ce fût le mérite de A. Fresnel d'avoir proposé une méthode de calcul basée sur la division de la figure en zones dites zones de Fresnel.
