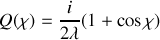Fresnel a utilisé une astuce de calcul pour calculer l'intégrale. Pour cela il a divisé la surface d'onde ou se trouve le point
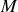en une série de zones
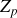. Chaque zone est obtenue en traçant les cercles de centre
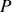et de rayons
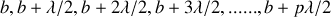où
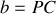(voir figure 6). Il remarque alors que les rayons lumineux issus de deux zones consécutives sont en opposition de phase puisque leur trajet optique diffère de
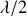. Il s'ensuit que deux zones consécutives s'annihilent entre elles. De ce fait si l'on part de la première zone et que l'on somme toutes les contributions des autres zones, celles ci se détruisent deux à deux et il ne reste schématiquement que la contribution de la première zone.
Remarque :
Pour faire le calcul de la contribution d'une zone quelconque on suppose que la longueur d'onde est suffisamment petite par rapport à
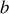et
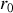pour que le facteur d'obliquité soit constant dans chaque zone ; il est alors noté
.
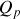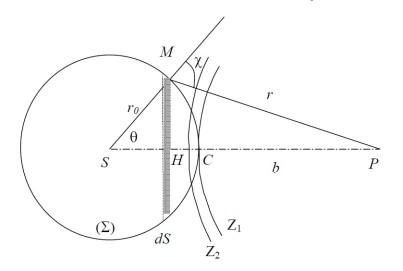
Fresnel a ensuite calculé la contribution de chaque zone
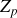au point
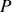et il a ensuite sommé toutes les contributions pour trouver le résultat final. Pour une position quelconque de
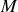sur la sphère
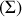on a
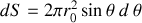
L'identité d'Alkachi appliquée dans le triangle SPM conduit à
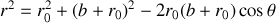
ce qui entraîne
Il s'ensuit que
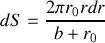
La contribution élémentaire de la zone
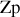au champ en
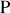est donc
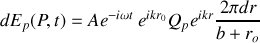
ce qui conduit à
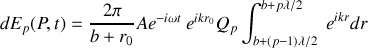
Après intégration il vient
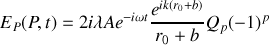
Le champ total au point
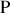est obtenu en sommant contribution de toutes les zones de Fresnel ce qui conduit à
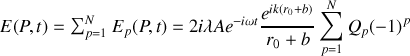
Pour déterminer le champ en
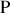il convient ensuite d'évaluer la valeur de la suite. Fresnel a montré que cette suite peut s'écrire
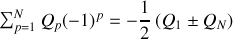
Or si l'on considère la sphère la dernière zone correspond à
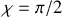ce qui entraîne
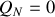. Il s'ensuit que le champ en
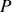est égal au champ créé par la première zone de Fresnel et vaut
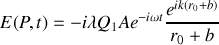
Si l'on considère un rayon allant directement de
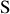en
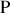le champ est aussi égal à
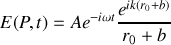
ce qui montre que
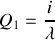
Remarque :
En principe il convient de traiter le problème vectoriellement à cause de la polarisation de la lumière d'une part et d'autre part à cause du caractère vectoriel du champ (les champs qui se superposent en
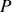ne sont pas colinéaires). La théorie de Fresnel reste cependant une théorie scalaire non rigoureuse mathématiquement. Le calcul rigoureux de la diffraction par une ouverture est extrêmement compliqué et ne sera pas abordé dans ce cours. Pour des quantités scalaires, il faut pour cela utiliser la
théorie de Kirchhoff qui permet de montrer que le facteur d'obliquité est égal à
