Nous considérons dans cet exemple le calcul de la figure de diffraction d'une onde plane par une fente de largeur finie
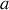 . L'onde incidente est supposée être une onde plane progressive ce qui impose que tous les points lumineux arrivant sur la fente y arrivent en phase car ils sont tous contenus dans le même plan d'onde.
. L'onde incidente est supposée être une onde plane progressive ce qui impose que tous les points lumineux arrivant sur la fente y arrivent en phase car ils sont tous contenus dans le même plan d'onde.
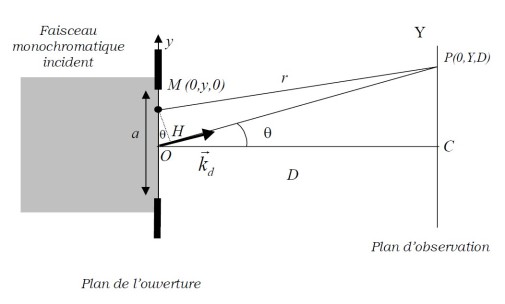
A la traversée de la fente, la présence des bords de la fente conduisent au phénomène de diffraction c'est à dire que l'onde plane progressive perd son caractère d'onde plane pour se transformer en onde sphérique. Un point
 de l'écran d'observation recevra une infinité de rayons lumineux provenant de tous les points du diaphragme. Ces points émettent des ondes sphériques synchrones. Comme la distance qui sépare deux points distincts du diaphragme au point
de l'écran d'observation recevra une infinité de rayons lumineux provenant de tous les points du diaphragme. Ces points émettent des ondes sphériques synchrones. Comme la distance qui sépare deux points distincts du diaphragme au point
 n'est pas la même les ondes issues de ces deux points vont arriver en
n'est pas la même les ondes issues de ces deux points vont arriver en
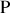 avec un certain déphasage. Nous avons vu que le déphasage en
avec un certain déphasage. Nous avons vu que le déphasage en
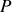 entre l'onde issue du point
entre l'onde issue du point
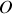 et cette même onde issue du point
et cette même onde issue du point
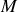 est donné par :
est donné par :
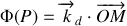
L'expression de la diffraction à distance infinie conduit à :
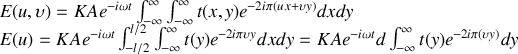
En effet nous supposons que le trajet du faisceau ne soit pas altéré dans la direction
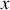 parallèle aux arêtes de la fente et que le diamètre du faisceau soit
parallèle aux arêtes de la fente et que le diamètre du faisceau soit
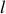 . Il n'y a donc pas de diffraction dans la direction
. Il n'y a donc pas de diffraction dans la direction
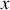 et le terme de phase disparaît ipso facto. La transparence de la pupille est nulle en tout point de la fente se situant en dehors de l'intervalle
et le terme de phase disparaît ipso facto. La transparence de la pupille est nulle en tout point de la fente se situant en dehors de l'intervalle
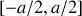 et vaut 1 dans cet intervalle. Il en résulte que :
et vaut 1 dans cet intervalle. Il en résulte que :
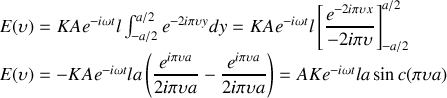
Si l'on revient à la variable de position
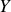 sur l'écran qui s'écrit à partir de
sur l'écran qui s'écrit à partir de
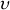 :
:
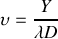
nous obtenons l'amplitude diffractée en
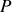 suivante :
suivante :
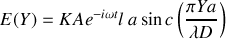
L'intensité diffractée en
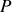 est donc égale à :
est donc égale à :
La figure 11 représente l'intensité diffractée par la fente dans le plan de l'écran.
On retrouve bien le fait que l'intensité observée sur l'écran est constituée d'un lobe principal deux fois plus large que les lobes latéraux et que l'intensité des lobes latéraux est beaucoup plus faible que celle du lobe principal.
Remarque :
la figure de diffraction est d'autant plus étalée que la largeur de la fente est petite. L'étalement de la figure de diffraction est inversement proportionnel à l'ouverture de la fente.
D'autre part l'intensité au centre de la figure est proportionnelle à
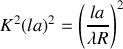 ce qui montre que l'intensité au centre décroît comme le carré de la distance de la fente à l'écran et croît comme le carré de la surface de l'ouverture. Une figure de diffraction sera donc d'autant plus lumineuse que l'ouverture de la fente sera grande.
ce qui montre que l'intensité au centre décroît comme le carré de la distance de la fente à l'écran et croît comme le carré de la surface de l'ouverture. Une figure de diffraction sera donc d'autant plus lumineuse que l'ouverture de la fente sera grande.




