Le calcul de la diffraction par une pupille circulaire est basé sur le même principe que celui d'une pupille rectangulaire. Toutefois il importe d'utiliser la symétrie de la pupille pour parfaire le calcul. En partant de la relation générale
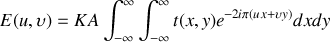
nous introduisons les coordonnées cylindriques
,
pour décrire la position du point
de sorte que
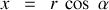
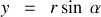
Nous avons donc
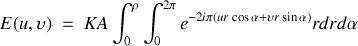
La figure de diffraction ayant la symétrie cylindrique de la pupille nous ne considérons le calcul que dans la direction
ce qui conduit à
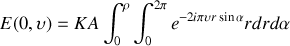
Nous utilisons ensuite la définition de la fonction de Bessel d'ordre
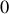donnée par
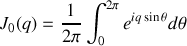
ce qui nous amène à
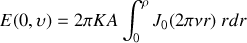
L'intégrale de la fonction de Bessel d'ordre zéro s'obtient ensuite en utilisant la propriété suivante de cette fonction
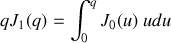
soit en posant
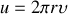
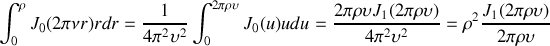
Il s'ensuit que
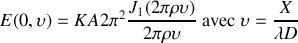
L'intensité qui est observée sur l'écran distant de
de la pupille circulaire s'écrit donc
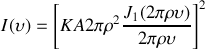
Les fonctions de Bessel sont tabulées et le premier zéro de la fonction
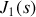est localisé en
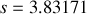. Il s'ensuit que l'intensité s'annule en
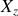
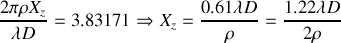
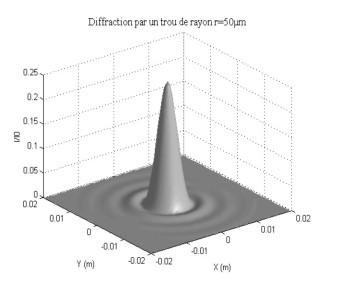
La figure 13 illustre le comportement de la fonction de Bessel au carré. On constate que la figure de diffraction est représentée par un lobe principal très intense et des lobes secondaires très très faibles. Le premier lobe secondaire culmine à 1.75% de l'intensité du lobe principal. Les autres lobes ne sont pas visibles sur un dessin présenté en échelle linéaire. La lumière diffractée par un trou circulaire est donc presque intégralement concentrée dans le lobe principal délimité par un anneau sombre de diamètre angulaire
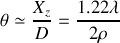
La symétrie de révolution de la pupille se retrouve dans la figure de diffraction qui présente l'allure d'un disque central entouré d'anneaux concentriques d'intensité de plus en plus faible. Le disque central pèse pour 84% de l'intensité totale et son rayon est donné par l'équation
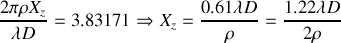. Ce disque s'appelle le disque d'Airy.
Attention :
Il est important d'en connaître les caractéristiques car de nombreux instruments d'optiques sont formés de pupilles circulaires (lunette astronomique, microscopes...). Dans tous ces instruments la diffraction est un facteur limitant la résolution. La figure 13 montre l'allure de la figure de diffraction d'une pupille circulaire.
