Deux ondes lumineuses arrivant en un point
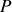de l'espace peuvent interférer en ce point si il existe au cours du temps une relation de phase constante entre ces deux ondes. Quand cela est vérifié l'intensité mesurée au point d'interférence n'est pas égale à la somme des intensités lumineuses de chacune des ondes qui arrivent en
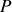mais au module au carré de la somme des amplitudes des deux ondes.
Si l'amplitude instantanée de chaque onde est donnée par :
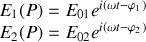
l'intensité de chaque onde prise séparément est alors donnée par :
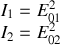
et l'intensité résultant de la superposition de ces ondes en
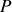est donnée par :
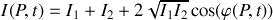
Par la suite, nous ne considérerons que des ondes de même état de polarisation et se superposant sous un angle faible ce qui revient à utiliser des ondes scalaires. De plus nous ferons l'hypothèse que les ondes ont la même amplitude. Dans ce cas, l'intensité résultant en
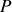à l'instant
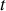donné est :
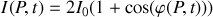
Remarque :
Si l'on considère un observateur regardant l'intensité lumineuse en
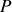, celui-ci n'est capable de percevoir l'intensité lumineuse que sur un temps de quelques secondes voir au mieux de quelques dixièmes de secondes. Or nous avons vu que le temps d'émission d'un train d'onde est de l'ordre de quelques nano secondes. Ainsi notre observateur ne perçoit-il que la moyenne temporelle des intensités provenant de milliards de trains d'onde. La moyenne temporelle de l'intensité est donnée par :
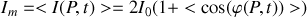
Ce qui montre que le terme de phase qui est la source de l'observation des interférences ne persistera que si la différence de phase entre les deux ondes est constante dans le temps. Dans ce cas, l'intensité résultante en
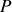est donnée par :
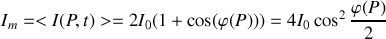
L'expression écrite ci-dessus ne prend pas en compte l'origine même de la superposition des ondes à savoir la diffraction.
La figure d'interférence qui résulte de la superposition des ondes diffractées par les fentes d'Young peut être calculée à partir du formalisme général de la diffraction. Nous allons montrer dans le calcul qui suit comment il est possible d'analyser la contribution des interférences et de la diffraction dans l'expérience d'Young.
