Utilisation de la transparence
En prenant l'origine des phases sur le plan d'onde arrivant sur les fentes d'Young, on peut écrire que les champs électriques en
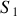et
sont :
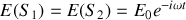
Les deux champs ont exactement la même phase et la même amplitude puisque :
ils proviennent du même plan d'onde
ils sont issus de fentes de même ouverture
L'amplitude du champ résultant en
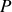est donnée par la transformée de Fourier de la transparence des fentes d'Young multipliée par l'amplitude du champ incident soit :
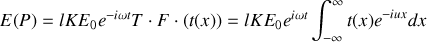
En introduisant la fréquence spatiale
dans le calcul de l'intensité, il vient :
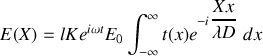
La transparence des fentes d'Young est nulle partout sauf à la position des ouvertures ou elle vaut 1.
Comme le montre la figure Nous avons ainsi :
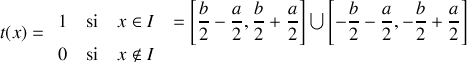
Il en résulte que le champ en
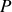est égal à :
L'intégration des exponentielles est immédiate et conduit à :
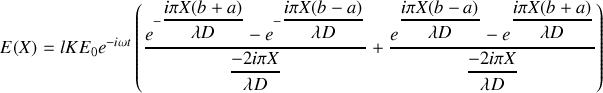
soit
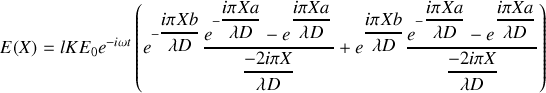
ce qui conduit à :
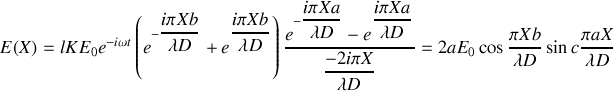
L'intensité diffractée en
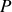est donc égale à :
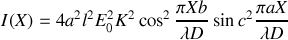
ce qui peut aussi se mettre sous la forme
On retrouve dans cette expression un terme d'interférence représenté par le cosinus au carré qui résulte de la superposition des ondes issues des sources synchrones
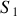et
distantes de
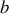, et un terme de diffraction par une fente de largeur
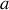représenté par le sinus cardinal au carré.
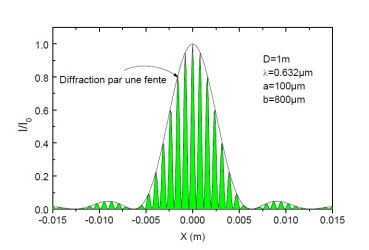
La figure ci-dessous est un exemple de la figure de diffraction obtenue pour des fentes d'Young distantes de 0.8mm d'ouverture 0.1mm éclairées à l'aide d'un Laser He-Ne à un mètre de distance.
La fonction d'interférence évolue entre 0 et 1 et s'annule à chaque fois que :
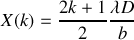
ce qui conduit à un interfrange
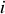donné par :
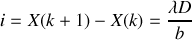
La fonction de diffraction par une fente de largeur
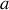caractérisée par le sinus cardinal est par contre une fonction décroissante de
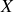qui s'annule à chaque fois que :
On voit ainsi que la figure d'interférences qui, si l'on ne tenait pas compte de la diffraction s'étendrait à l'infini, est sérieusement limitée par la diffraction. En effet nous savons déjà que l'intensité maximale du premier lobe latéral de diffraction ne représente que 4.7% de l'intensité maximale du premier ; il s'ensuit que la figure d'interférences est de moins en moins visible au fur et à mesure que l'on s'éloigne du centre de l'écran (figure 10).
Cas particulier de fentes très fines
Nous supposons maintenant que les fentes sont extrêmement fines
. Dans ce cas il est clair que le lobe principal de diffraction sera très étendu et que le phénomène d'interférences sera assez visibles sur une large étendue de l'écran.
Remarque :
Réduire l'ouverture des fentes a pour effet de réduire l'intensité lumineuse sur l'écran puisque l'intensité au centre est proportionnelle à
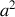. Si
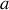est suffisamment petit, la diffraction peut être négligée et on ne voit plus que la figure d'interférences
Nous nous plaçons donc dans cette hypothèse et nous examinons successivement ce qui va se produire si l'on incline les rayons lumineux sur l'axe principal et s'il l'on utilise une source polychromatique.
Rayons inclinés sur l'axe principal
Si l'inclinaison est nulle nous avons
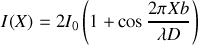
L'argument du cosinus n'est rien d'autre que la différence de phase entre les ondes issues des sources
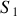et
. Si maintenant on incline les rayons incidents d'un angle
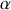par rapport à l'axe principal passant par le centre des fentes nous sommes tenus d'introduire un déphasage supplémentaire qui tient compte du fait que l'onde qui arrive en
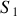n'est pas en phase avec celle qui arrive en
mais présente un déphasage égal à
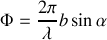
Nous notons que ce déphasage est constant pour autant que l'angle
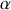le soit. Il en résulte que l'intensité en un point
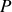de l'écran devient égale à
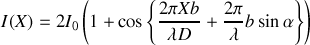
Si l'on suppose que l'onde plane inclinée est obtenue en positionnant une source ponctuelle au foyer d'une lentille convergente de focale f, nous avons alors
et il s'ensuit que
La figure d'interférences est donc décalée du centre de l'écran de
.
