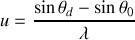Nous déterminons maintenant l'intensité diffractée par un réseau de traits éclairés de façon cohérente. Chaque trait du réseau est séparé de son voisin de la période du réseau. Il suffit pour faire le calcul complet de repartir de l'équation fondamentale de la diffraction à l'infini qui s'écrit pour des fentes rectilignes infinies :

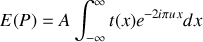
Il importe donc d'exprimer la fonction de transparence du réseau. La transparence totale peut être considérée comme étant la somme des fonctions de transparence de chaques fentes prises individuellement soit :

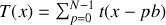
L'amplitude diffractée est la transformée de Fourier de la transparence des fentes soit :

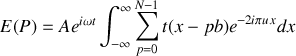
D'après la propriété de linéarité de l'intégrale, l'intégrale d'une somme est la somme des intégrales ce qui conduit à :

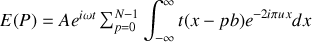
On utilise ensuite le changement de variable suivant :

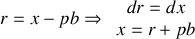
ce qui conduit à :

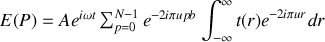
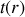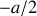Comme la fonction n'est non nulle que si est compris entre et 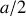il s'ensuit que

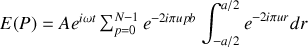
On voit alors apparaître le produit de la fonction d'interférences par la fonction de diffraction par une fente soit :

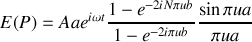
L'intensité diffractée a pour formulation :

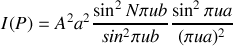
avec