Attention :
Connaissant les f.e.m. des générateurs et les résistances du réseau, résoudre celui-ci c'est déterminer l'intensité du courant qui circule dans chacune des branches.
Il existe
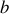branches dans le réseau donc
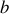courants inconnus. Les
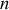nœuds et les
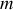mailles donnent a priori
équations. Comme en général
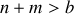, il faut trouver un système complet de b équations linéairement indépendantes.
Comme il existe
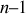nœuds indépendants, il faut étudier
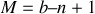mailles.
Equations pour les noeuds
Le nœud d'indice
est la jonction de
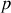branches (d'indice
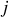) parcourues par des courants
.
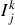La loi de conservation de l'électricité (première loi de Kirchhoff ) s'écrit sous la forme algébrique suivante :
Equations des mailles
La maille d'indice
contient
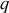branches. La différence de potentiel entre les extrémités de la branche
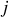s'écrit
.
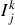Comme la maille constitue un parcours fermé, on a (seconde loi de Kirchhoff) :
En procédant uniquement à des regroupements en série, on peut transformer toute branche j de la maille k en un générateur de f.e.m.
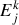en série avec une résistance
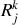parcourue par le courant
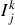. (Si la branche ne contient pas de générateur alors
). La loi des mailles peut donc aussi s'écrire sous la forme :
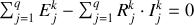
Les sommes sont des sommes algébriques et l'écriture correcte des signes des différences de potentiel constitue la seule difficulté du problème.
Remarque :
La méthode la plus rationnelle consiste à faire le choix d'un sens de parcours sur la maille étudiée (choix arbitraire) et à choisir pour chaque branche un sens pour le courant. La f.e.m. d'un générateur est comptée avec le signe de la borne par laquelle on entre dans celui-ci. Les d.d.p. aux bornes des résistances sont positives si le courant dans la branche a le même sens que le sens de parcours et négatives dans le cas contraire. On écrit que la somme des tensions est nulle. Si à l'issue du calcul, on obtient pour le courant d'une branche une valeur négative, c'est que le courant réel de cette branche circule dans le sens opposé à celui qui a été choisi. Si la branche contient un récepteur polarisé, il faut faire l'étude pour les deux sens du courant. Selon celui-ci, le "récepteur" se comporte soit comme un récepteur soit comme un générateur.
On obtient un système linéaire de
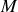équations à
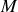inconnues de la forme :
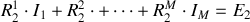
qui peut s'écrire sous la forme matricielle suivante :
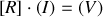
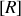est une
matrice dont la dimension des éléments est celle d'une résistance.
et
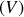sont des vecteurs colonnes à
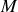éléments.
