Méthode générale
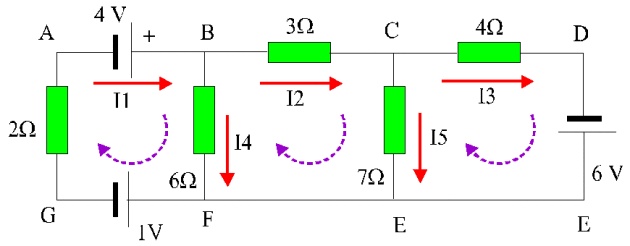
On cherche les courants dans toutes les branches du circuit de la figure 14.
Le choix du sens des courants dans les 5 branches est arbitraire. Il y a pour cet exemple trois courants à calculer
,
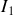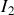et
car la loi des nœuds en
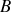et
donne :
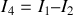et
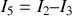
Les flèches en pointillés violets indiquent les sens de parcours, choisis arbitrairement, des 3 mailles étudiées.
Pour la maille
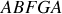, on obtient :
Soit :
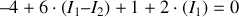
De même :
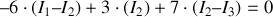(maille
)
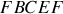(maille
)
D'ou la représentation matricielle du système :
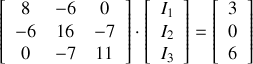
Pour résoudre ce système linéaire, il suffit d'inverser la matrice : on la transpose, puis on remplace dans la transposée chaque terme par son cofacteur(attention au signe) divisé par le déterminant. On peut aussi utiliser un logiciel spécialisé.
Cliquez ici pour résoudre cet exemple.
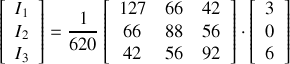
Résolution par la méthode de Kramer : (pour obtenir la variable k, on divise le déterminant de la matrice obtenue en remplaçant la ke colonne par la colonne des constantes par le déterminant de la matrice initiale.
Remarque :
Comme
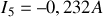est négatif, le courant dans la branche
circule dans le sens contraire à celui de la flèche de la figure 14. Les courants réels
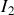et
circulent dans le sens contraire des flèches.
Méthode par substitutions
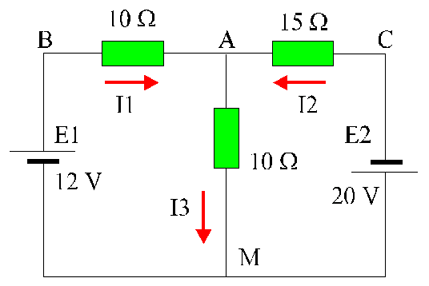
On cherche à déterminer
Mise en équation :
maille
:
(a)maille
:
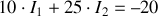(b)
Résolution :
De la différence (a) – 2.(b), on tire :
soit
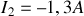
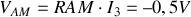
et donc :
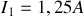et
