A la grandeur scalaire
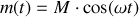, on associe le vecteur
de module
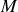qui tourne autour de
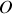avec la vitesse
.
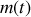est la projection
de sur l'axe
.
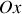A une seconde grandeur
est associé un vecteur
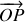déphasé de j par rapport au vecteur
Dans cette représentation, on associe donc des vecteurs tournants aux grandeurs électriques sinusoïdales (courants et tensions). On utilise les propriétés géométriques de la figure obtenue pour la résolution du problème.
Exemple :
Pour effectuer la somme de deux tensions, on fait la somme vectorielle de leurs vecteurs représentatifs. La tension résultante est la projection du vecteur obtenu sur l'axe
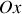. Cette construction donne aussi les phases relatives des diverses grandeurs.
Attention :
La représentation de Fresnel, très utilisée en optique physique, n'est facilement exploitable en électricité que pour des circuits très simples.
