L'analogie entre le plan de Fresnel et le plan complexe conduit naturellement à représenter les vecteurs tournants associés aux grandeurs électriques sinusoïdales par des grandeurs imaginaires.
Notations
Une grandeur complexe
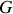sera notée
et son complexe conjugué
.
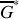Les intensités étant souvent nommées avec la lettre
, pour éviter toute confusion le symbole des imaginaires est noté en électricité avec un
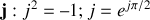
La partie réelle de
est notée
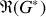, la partie imaginaire est notée :
Au vecteur
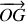du plan
, on associe le nombre complexe
Ainsi à l'intensité
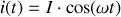, on fait correspondre
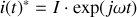
A la tension
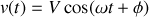, on fait correspondre
Dans la suite, nous prendrons l'intensité comme origine des phases.
Attention :
La grandeur physique est la partie réelle de la grandeur complexe associée.
En effet :
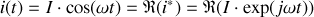
De même :
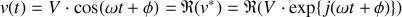
Amplitude complexe
Soit
. On pose
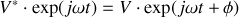
On définit ainsi l'amplitude complexe
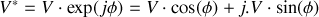
Impédance complexe
Par analogie avec la loi d'Ohm, on définit l'impédance complexe
, d'un dipôle, comme étant le quotient de
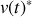par
:
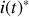est une résistance ;
est une réactance.
Le module de l'impédance est
; la phase de l'impédance est
.
On a également :
et
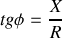avec
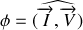
Admittance complexe
Par analogie avec la conductance
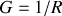, on définit l'admittance complexe
(
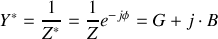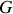est une conductance et
une susceptance). On a :
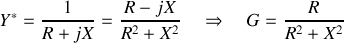
et
