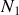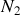On admet que les inductances sont des solénoïdes de section S ayant et spires, des longueurs 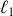et 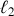et que les pertes sont négligeables. Si est le flux d'induction à travers l'enroulement primaire, on a :

;

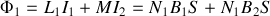
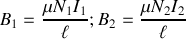
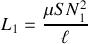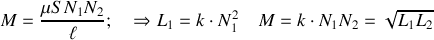
Avec ces hypothèses, on obtient en régime sinusoïdal :

Figure 6

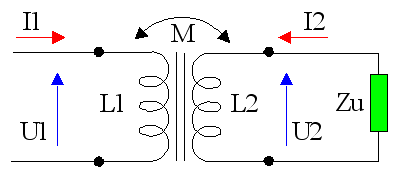
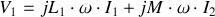
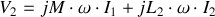
A partir de l'expression de la matrice du transformateur, on détermine l'expression de l'impédance vue à l'entrée quand le transformateur est chargé par une impédance .

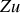Soit :

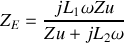
Cette impédance est équivalente à une impédance 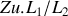en parallèle avec une impédance 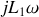. Si le produit 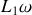est assez grand, l'impédance présentée par le transformateur chargé est donc 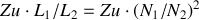. ( est le rapport de transformation).

Le transformateur permet donc l'adaptation en puissance des impédances entre une source d'impédance 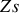et une charge d'impédance 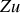. Il suffit d'utiliser un transformateur de rapport .