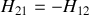Pour les quadripôles ne contenant que des dipôles linéaires les 4 grandeurs fondamentales
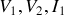et
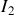sont liées par des équations linéaires.
Plusieurs représentations matricielles sont possibles et le choix de l'une de celles-ci sera fait en fonction du problème étudié.
Matrice impédance
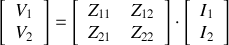
On exprime les tensions en fonction des courants. Les éléments de la matrice ont la dimension d'impédances.
Matrice admittance
On exprime les courants en fonction des tensions. Les éléments de la matrice ont la dimension d'admittances.
Matrice de transfert
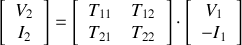
On exprime les grandeurs de sortie en fonction des grandeurs d'entrée.
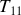est un nombre,
est une impédance,
une admittance et
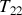un nombre.
Rappel :
Bien noter dans cette représentation le signe moins affecté à
.
La matrice inverse de la matrice de transfert donne les paramètres d'entrée en fonction des paramètres de sortie.
Matrice hybride
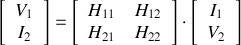
L'intérêt de cette représentation apparaît lors de l'étude des transistors.
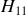est une impédance,
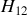est un nombre,
un nombre et
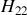une admittance. On utilise parfois la matrice
.
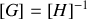Les relations étant linéaires, il est facile de déduire les coefficients d'une représentation à partir de ceux d'une autre.
Caractéristiques des quadripôles passifs
Ce sont les réseaux de courbes qui représentent les variations des tensions en fonction des courants. Par exemple, pour le réseau
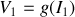, on prendra
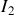ou
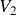comme paramètre : chaque courbe de ce réseau est tracée pour une valeur donnée et constante de
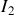(ou de
).
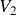Propriété des quadripôles passifs
Soit un quadripôle passif dont la tension d'entrée est
et le courant de court-circuit en sortie est
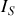. D'après le théorème de réciprocité, le courant dans l'entrée en court-circuit est
si la tension de sortie est
.
Les relations entrée
sortie pour la matrice de transfert s'écrivent :
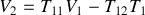
Sortie en court-circuit :
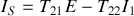
Entrée en court-circuit :
L'égalité
implique que :
.
Des calculs analogues montrent que pour un quadripôle passif on a aussi :
et
