Multiplicateur
Pour compenser les effets des courants d'entrée, on relie l'entrée non inverseuse à la masse par une résistance R_3 = R_1 // R_2. Le courant qui circule dans cette résistance étant très faible, le potentiel de l'entrée + est celui de la masse. Le potentiel du point A est également nul car V^+ = V^–, mais l'impédance entre le point A et la masse n'est pas nulle. On dit que ce point est une masse virtuelle.
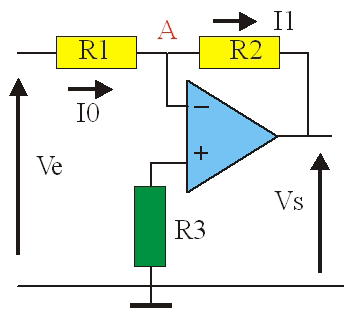
I_1 = (V_A – V_S)/R_2 \qquad I_0 = (V_E – V_A)/R_1
Le courant vers l'entrée – est nul donc : I_0 = I_1
Comme V_A = V^+ = 0, on tire :
I_0 = V_E/R_1 = – V_S/R_2 \Rightarrow V_S=-\frac{R_2}{R_1}V_E
Le gain est négatif. Il y a un déphasage de \pi entre l'entrée et la sortie en régime sinusoïdal.
Le courant d'entrée du montage étant I_0, l'impédance d'entrée est égale à R_1.
Sommateur
Si l'amplificateur opérationnel est idéal le courant dans R_P est nul et V^– = V^+ = 0
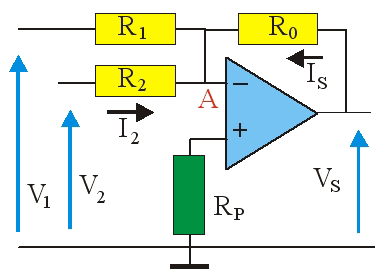
On pose : I_S = (V_S – V_A)/R_0
I_1 = (V_1 – V_A)/R_1 \qquad I_2 = (V_2 – V_A)/R_2
Or : \SigmaI_A = 0 \,\,\,et \,\,\, V_A = 0
V_S/R_0 = – (V_1/R_1 + V_2/R_2)
V_S=R\cdot\left(\frac{V_1}{R_1}+\frac{V_2}{R_2}\right)
En choisissant R_1 = R_2 = R_0, on obtient V_S = – (V_1 + V_2).
Toujours pour compenser les effets des courants d'entrée, il est conseillé de relier l'entrée non inverseuse à la masse par une résistance R_P = (R_0 // R_1 // R_2).
Ce montage est souvent utilisé comme « mélangeur » de signaux.
Intégrateur idéal
Le signal d'entrée est V_E(t). Dans le modèle idéal, V_A = 0 ; donc : i(t) = V_E(t)/R
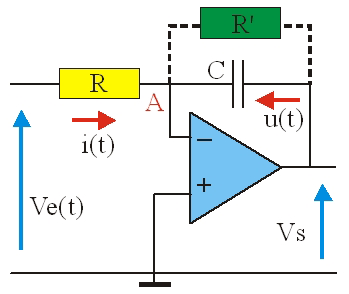
Le courant dans le condensateur est : i(t) = – C.dV_S/dt
\frac{dV_S}{dt}=-\frac{1}{RC}V_E
Par intégration, on tire : V_S=K-\frac{1}{RC}{\displaystyle\int^t_o}V_E(\theta)d\theta
En fait, ce montage ne fonctionne pas correctement : le faible courant d'entrée de l'amplificateur produit dans R une chute de tension qui est elle aussi intégrée : la sortie se sature car le condensateur reste chargé. Pour obtenir une intégration satisfaisante, on peut placer une résistance R' en parallèle sur C afin de permettre l'écoulement de son courant de décharge. Cette résistance doit être assez grande pour ne pas perturber l'intégrateur mais pas trop pour pouvoir jouer son rôle. En pratique on prend R' \approx10\cdotR.
Dérivateur idéal
Par permutation du condensateur et de la résistance, on obtient un dérivateur.
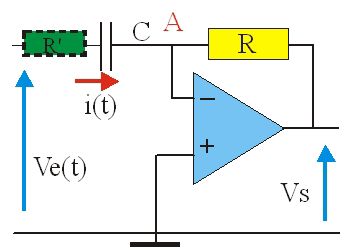
Le courant dans le condensateur est : i(t) = dQ(t)/dt = C\cdotdV_E(t)/dt
C'est aussi le courant qui circule dans la résistance R : V_S(t) = –R\cdoti(t)
Donc : V_S(t)=RC\cdot\frac{dV_E(t)}{dt}
La tension de sortie est proportionnelle à la dérivée de la tension d'entrée. En pratique, R et C sont choisis en fonction de la fréquence du signal pour obtenir un gain compris entre 0,1 et 10. Ce montage est insensible à la dérive mais il a tendance à osciller en haute fréquence. Pour y remédier, on peut placer une résistance R' en série avec le condensateur (R' < R/10) qui limitera le gain aux fréquences élevées et donc les possibilités d'oscillation.
Convertisseur tension-courant
On utilise le fait que les courants qui circulent dans la résistance R et dans une charge, placée entre A et la sortie, sont identiques. V_A = 0 \Rightarrow I = V_E /R
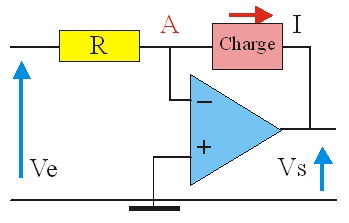
Ce courant est donc indépendant de la nature et de la valeur de l'impédance de la charge. Le montage est équivalent à un générateur de courant commandé par une tension. La réalisation pratique d'un tel convertisseur s'écarte souvent de ce schéma de principe car le courant de sortie de l'amplificateur opérationnel est limité.
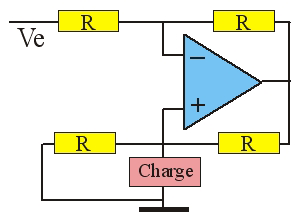
Pour ce montage, nommé source de Howland, montrer que si les 4 résistances R sont égales, le courant dans la charge est égal à :
I = – V_E /R
Convertisseur courant-tension
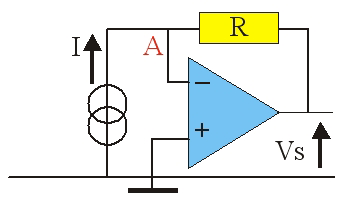
On relie le point A à un générateur de courant d'intensité I. On a donc :
V_S = – R\cdotI
Le montage se comporte en générateur de tension commandé par un courant.
Un tel montage peut être utilisé pour amplifier le courant d'une photodiode.