On réalise le circuit de la figure 21 dans lequel R_2 introduit une réaction positive. L'amplificateur fonctionne donc en régime de saturation.
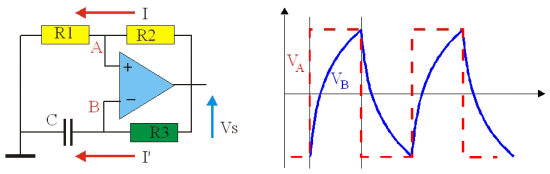
Principe du fonctionnement
Si V_A > V_B , on a : V_S = + U. Le condensateur C se charge à travers R_3. Le potentiel du point B croît jusqu'à la valeur V_A (R_1 et R_2 forment un pont diviseur), puis le montage bascule et alors V_S = – U.
Le potentiel de A devient négatif et donc : V_A < V_B. Le condensateur se décharge à travers R_3. V_B décroît jusqu'à ce qu'il devienne inférieur à V_A et le montage bascule à nouveau. Le système oscille indéfiniment entre ces deux états (astable) avec une période fonction des valeurs des éléments du circuit.
Calcul de la période
On suppose que initialement V_S = + U
V_A = V_S\cdotR_1/(R_1 + R_2) \qquad\qquad (a)
R_3\cdotI' = V_S – V_B = R_3\cdotC\cdotd(V_B)/dt \qquad\qquad (b)
La solution générale de l'équation (b) est : V_B = K\cdotexp(– t/\tau) avec tau = R_3C
Une solution particulière est : V_B = V_S = +U
La solution générale est donc : V_B = +U + K\cdotexp(– t/\tau)
On prend comme origine des temps, l'instant où le système a basculé ; en t = 0 on a : V_B(0) = – V_A = – U\cdotR_1/(R_1 + R_2)
K = V_B(0) – U = – U\cdot[1 + R_1/(R_1 + +R_2)] = – U\cdot(2\cdotR_1 + R_2)/(R_1 + R_2)
V_B=U-U\frac{2R_1+R_2}{R_1+R_2}e^{-\frac{t}{\tau}
En t = 0 : V_B = – U\cdotR_1/(R_1 + R_2) ; V_B croit jusqu'à t = t_1= T/2 pour atteindre la valeur V_B = + U\cdotR_1/(R_1 + R_2)
U\cdotR_1/(R_1 + R_2) = U – U\cdot[(2\cdotR_1 + R_2)/(R_1 + R_2)]\cdotexp(– t_1/\tau)
[(2\cdotR_1 + R_2)/(R_1 + R_2)]\cdotexp(– t_1/\tau) = R_2 /(R_1 + R_2)
(2\cdotR_1 + R_2)\cdotexp(– t_1/\tau) = R_2 \Rightarrow exp(t_1/\tau) = 1 + 2\cdotR_1/R_2
t_1 = \tau\cdotLn\,(1 + 2\cdotR_1/R_2)
L'expression de la période est donc : T= 2R_3C\cdot\,Ln\left(1+\frac{R_1}{R_2}\right)
Ce circuit constitue un oscillateur et génère une tension rectangulaire. Ici encore il importe d'utiliser un amplificateur opérationnel dont le temps de montée est le plus petit possible.