Par rapport au montage précédent, on permute C et R_1

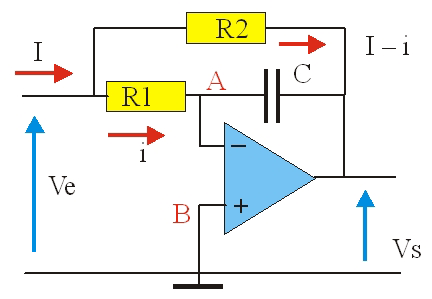
V_A = V_B = 0

I = i + (I – i)

V_E = R_1\cdoti \qquad V_S = – i/jC\omega

V_S = – V_E/jC\cdot\omega\cdotR_1

V_E – V_S = R_2\cdot(I – i)

I = i + (I – i)\cdot \,\,\,\, = V_E/R_1 + (V_E – V_S)/R_2

On en déduit la valeur du courant I.

I=V_E\cdot\left(\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{jC\omegaR_1R_2}\right)

La valeur de l'admittance équivalente est : Y_e=\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{jC\omegaR_1R_2}=\frac{1}{r}+\frac{1}{jL\omega}