On note
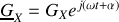la grandeur complexe associée à une grandeur temporelle
.
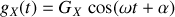On considère le montage en pont de Wheatstone représenté sur la Figure 3. Le générateur délivre une tension sinusoïdale de pulsation
,
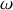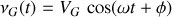(grandeur complexe associée
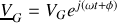) et on supposera son impédance interne négligeable. Les dipôles
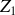à
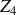ont pour impédance complexe les valeurs
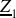à
.
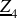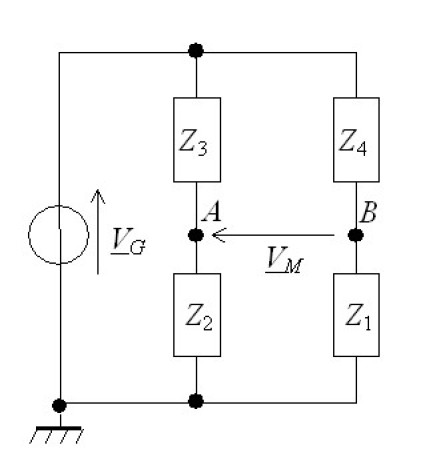
Question 1
Établir l'expression de la tension de sortie du pont,
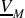, en fonction de la tension
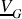et des quatre impédances
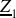à
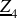. Vérifier que le pont est équilibré (tension de sortie nulle) lorsque
.
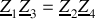Question 2
Les condensateurs
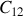et
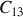sont montés en pont selon ce montage, respectivement à la place de
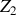et
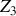. Les dipôles
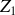et
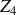sont des résistors, ayant la même valeur de résistance
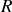. Redessiner le montage avec ces composants. Écrire les expressions des impédances
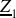à
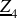en fonction de ces grandeurs (
,
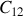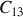et
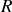) en notation « complexe ».
Question 3
Établir dans ce cas l'expression de la tension de sortie du pont,
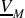, en fonction de
,
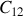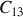et
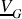. En déduire l'expression de
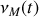. Préciser l'amplitu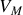de
de
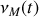en fonction de
,
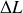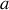et
.
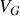