Les vitesses de deux points
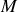 et
et
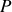 d'un même solide, en mouvement par rapport à un référentiel
d'un même solide, en mouvement par rapport à un référentiel
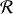 , sont liées par la relation vectorielle :
, sont liées par la relation vectorielle :
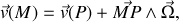
où
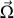 est un vecteur, appelé vitesse instantanée de rotation du solide, qui ne dépend que du temps. Cette relation entre les vitesses des différents points d'un solide permet de définir le torseur cinématique, ou torseur des vitesses, que nous noterons
est un vecteur, appelé vitesse instantanée de rotation du solide, qui ne dépend que du temps. Cette relation entre les vitesses des différents points d'un solide permet de définir le torseur cinématique, ou torseur des vitesses, que nous noterons
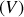 :
:
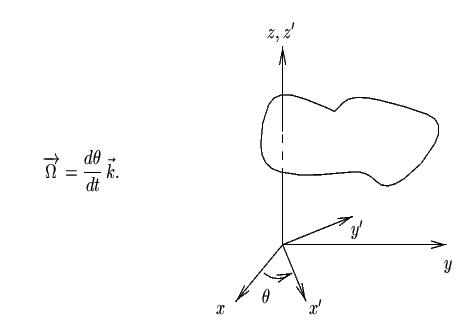
Dans le cas particulier de la rotation autour d'un axe fixe de directeur
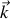 (
(
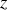 sur la figure suivante), le vecteur
sur la figure suivante), le vecteur
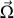 prend une valeur simple en fonction de la vitesse angulaire de rotation autour de l'axe
prend une valeur simple en fonction de la vitesse angulaire de rotation autour de l'axe
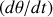 :
:
En pratique, le mouvement de rotation du solide est décomposé en une succession de rotations par rapport à des axes connus, de directeurs
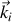 et auxquels sont associées les vitesses angulaires
et auxquels sont associées les vitesses angulaires
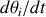 ; dans ces conditions on obtient comme vecteur vitesse instantanée de rotation du solide
; dans ces conditions on obtient comme vecteur vitesse instantanée de rotation du solide
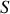
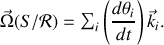
Dans le cas du passage d'un référentiel
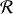 à un référentiel
à un référentiel
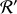 , la vitesse instantanée de rotation de
, la vitesse instantanée de rotation de
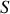 se transforme comme suit :
se transforme comme suit :
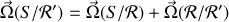
Exemple :
considérons un disque de centre
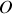 et de rayon
et de rayon
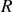 en rotation à la vitesse angulaire
en rotation à la vitesse angulaire
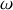 autour d'un axe perpendiculaire au disque passant par
autour d'un axe perpendiculaire au disque passant par
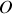 . Les dénominations des axes étant choisies comme sur la figure précédente, la vitesse instantanée de rotation s'écrit
. Les dénominations des axes étant choisies comme sur la figure précédente, la vitesse instantanée de rotation s'écrit
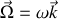 . Soit maintenant
. Soit maintenant
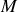 le point de la circonférence tel que
le point de la circonférence tel que
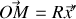 . La vitesse du point
. La vitesse du point
 étant nulle, l'application du torseur des vitesses entre
étant nulle, l'application du torseur des vitesses entre
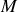 et
et
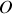 donne
donne
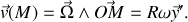
On retrouve qu'un point de la circonférence est animé d'une vitesse de module
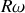 .
.




