Soient
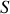et
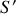deux solides 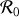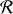et
,
et
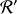trois référentiels dont le premier est fixe, lié à l'observateur et les deux suivants sont eux liés respectivement à
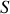et
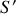(figure 1).
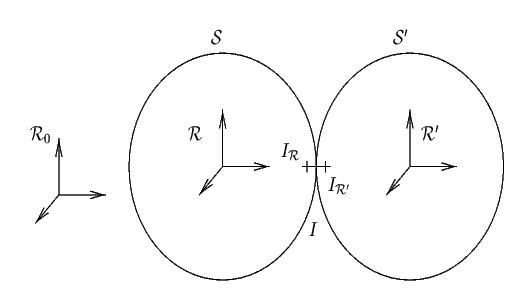
Définition :
On appelle vitesse de glissement
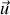de
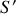par rapport à
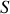la vitesse du point de contact
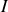lié à
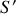, mesurée dans le référentiel lié à
:
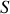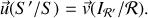
De la formule de composition des vitesses, on obtient
,
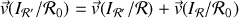soit pour la vitesse de glissement l'expression équivalente :
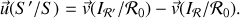
Si
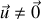, on dit qu'il y a glissement des deux solides l'un par rapport à l'autre et le vecteur
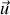appartient alors au plan
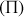tangent en
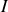et commun aux deux solides (figure 3).
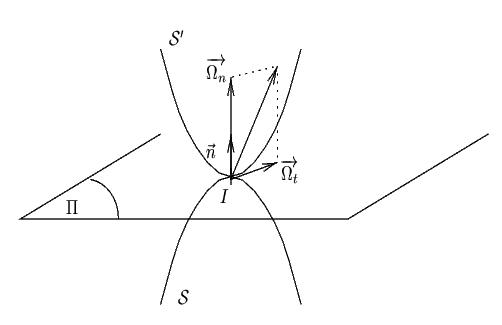
Décomposons le mouvement de rotation suivant les notations de la figure 3
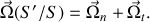
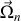, la composante normale au plan
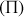du vecteur
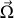est associée à un mouvement de pivotement, alors que la composante tangentielle
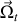est, elle, associée au roulement.
Exemple :
L'expression de la vitesse de glissement entre deux solides permet de retrouver rapidement les relations entre les vitesses angulaires de deux engrenages. On considère les deux engrenages
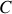et
de la figure suivante :
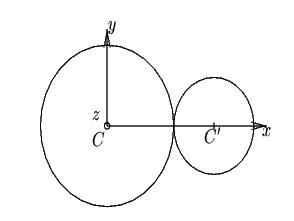
Leurs vecteurs rotation instantanée respectifs sont
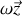et
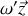. Soit
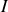le point de contact. La relation de non glissement entre les engrenages implique que
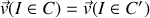, ce qui se traduit, compte tenu du calcul déjà effectué au paragraphe précédent, par :
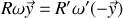. Les engrenages tournent bien en sens opposés, le plus petit effectuant la rotation à la plus grande des vitesses angulaires.
