Dans le cas d'un ensemble discret de masses :
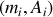 , le centre de gravité est défini au moyen de la formule
, le centre de gravité est défini au moyen de la formule
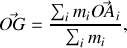
où
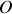 est un point arbitraire. Cette définition se généralise à une distribution continue de masse
est un point arbitraire. Cette définition se généralise à une distribution continue de masse
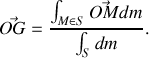
Pour une distribution volumique, l' élément de masse contenu dans un élément de volume
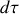 autour d'un point
autour d'un point
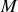 de
de
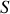 est
est
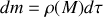 , où
, où
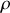 est la masse volumique du solide.
est la masse volumique du solide.
Exemple :
On cherche à calculer la position du centre de gravité d'un disque homogène (de centre
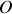 , de rayon
, de rayon
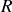 et de masse surfacique
et de masse surfacique
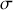 ), percé d'un trou circulaire de rayon
), percé d'un trou circulaire de rayon
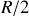 dont le centre
dont le centre
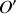 est à la distance
est à la distance
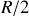 de
de
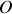 . Le calcul direct est fastidieux, alors que la propriété d'associativité du barycentre donne le résultat plus simplement. Le système est identique à la somme de deux sous systèmes : un disque plein de rayon
. Le calcul direct est fastidieux, alors que la propriété d'associativité du barycentre donne le résultat plus simplement. Le système est identique à la somme de deux sous systèmes : un disque plein de rayon
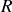 et de masse
et de masse
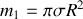 et un disque de rayon
et un disque de rayon
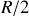 et de masse
et de masse
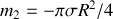 (l'équivalence est bien entendu mathématique, une masse ne pouvant être négative). Le centre de gravité de l'ensemble est le centre de gravité des barycentres partiels affectés de la masse totale de leurs sous-ensembles, à savoir
(l'équivalence est bien entendu mathématique, une masse ne pouvant être négative). Le centre de gravité de l'ensemble est le centre de gravité des barycentres partiels affectés de la masse totale de leurs sous-ensembles, à savoir
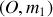 et
et
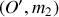 . Ainsi, pour tout point
. Ainsi, pour tout point
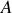 ,
,
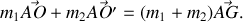
On peut choisir
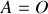 , d'où
, d'où
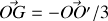 .
.
Définition :
On définit le référentiel barycentrique
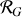 comme le référentiel d'origine
comme le référentiel d'origine
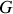 dont les axes sont parallèles à ceux de
dont les axes sont parallèles à ceux de
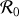 (référentiel de l'observateur ou du laboratoire).
(référentiel de l'observateur ou du laboratoire).
Attention :
Ce référentiel n'est donc pas lié au solide, ses axes ne tournant pas avec ce dernier.




