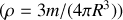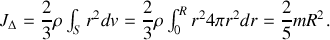On définit le moment cinétique
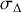de
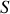par rapport à l'axe
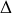de vecteur directeur
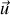par
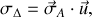
où
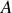est un point de
;
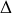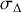est indépendant du choix de
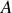. On définit de même le moment d'inertie de
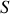par rapport à l'axe
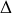au moyen de
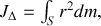
où
représente la distance à l'axe du point courant de
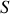. Une fois le moment d'inertie ainsi défini, on trouve que le moment cinétique par rapport à
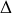a pour expression
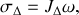
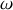étant la vitesse angulaire de rotation autour de
.
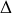Dans le cas où
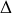est situé à une distance
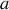de
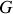, le théorème de Huygens permet d'écrire
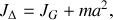
avec
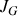moment d'inertie de
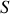par rapport à l'axe
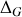parallèle à
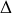et passant par
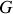(voir les problèmes II et III).
Exemple :
moment d'inertie d'une sphère pleine homogène de rayon
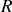et de masse
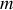par rapport à un de ses diamètres
.
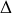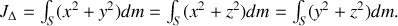
En sommant les trois expressions précédentes, il vient
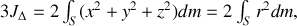
où
est la variable radiale des coordonnées sphériques. Soit
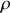la masse volumique de la sphère
