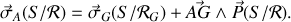Soit un solide
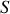de masse volumique
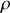et un référentiel
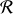. On définit le torseur cinétique de
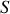dans
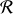par
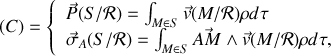
où la résultante
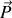est la quantité de mouvement de
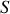dans
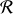et
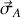le moment cinétique en
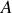de
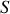dans
.
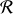En utilisant la définition du centre de gravité
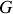, on montre que
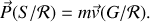
Il s'ensuit que la quantité de mouvement du solide
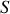dans son référentiel barycentrique est nulle.
De la relation de définition des torseurs, on déduit que
La relation de composition des vitesses entre
et
qui est en translation par rapport à
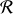nous donne
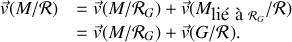
finalement on trouve ainsi que
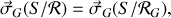
qui lorsqu'on utilise la relation des torseurs donne le théorème de Koenig du moment cinétique
